
|
| ¦Á |
|
| ¦Á1 |
| ¦Á2 |
| ¦Á |
| 3 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| ¦Á1 |
| ¦Á2 |
| ¦Á |
| ¦Á1 |
| ¦Á2 |
| ¦Á |
| ¦Á1 |
| ¦Á2 |
| ¦Á1 |
| ¦Á2 |
|
|
|
| ¦Á1 |
|
| ¦Á2 |
|
| ¦Á |
| ¦Á1 |
| ¦Á2 |
|
| ¦Á |
| ¦Á1 |
| ¦Á2 |
| ¦Á1 |
| ¦Á2 |
| ¦Ë | 5 1 |
| ¦Á1 |
| ¦Ë | 5 2 |
| ¦Á2 |
|
|
|
| 3 |
| 3 |
| |0+0-6| | ||||
|
|
|


 ѧϰʵĽůÔ°µŘϵÁĐ´đ°¸
ѧϰʵĽůÔ°µŘϵÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐżÎłĚ | Ä꼶 | łőÖĐżÎłĚ |
| ¸ßŇ» | ¸ßŇ»Ăâ·ŃżÎłĚÍĆĽöŁˇ | łőŇ» | łőŇ»Ăâ·ŃżÎłĚÍĆĽöŁˇ |
| ¸ß¶ţ | ¸ß¶ţĂâ·ŃżÎłĚÍĆĽöŁˇ | łő¶ţ | łő¶ţĂâ·ŃżÎłĚÍĆĽöŁˇ |
| ¸ßČý | ¸ßČýĂâ·ŃżÎłĚÍĆĽöŁˇ | łőČý | łőČýĂâ·ŃżÎłĚÍĆĽöŁˇ |
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
|
|
|
| 12 |
| 3cos2¦Č+4sin2¦Č |
|
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
| x2 |
| 4 |
| y2 |
| 9 |
| ¦Đ |
| 2 |
| ¦Đ |
| 3 |
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş¸Ł˝¨Ęˇ09-10ѧÄę¸ß¶ţĎÂѧĆÚĆÚÄ©ĘýѧŔíżĆżĽĘÔĘÔĚâ ĚâĐÍŁş˝â´đĚâ
Ł¨ą˛2СĚâ×ö´đŁ¬ĂżĐˇĚâ7·ÖŁ©
1Ł®Ł¨ŃˇĐŢ4ˇŞ2 ľŘŐóÓë±ä»»Ł©Ł¨±ľĚâÂú·Ö7·ÖŁ©
±ä»»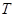 ĘÇ˝«Ć˝ĂćÉĎĂż¸öµă
ĘÇ˝«Ć˝ĂćÉĎĂż¸öµă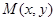 µÄşá×ř±ęłË2Ł¬×Ý×ř±ęłË4Ł¬±äµ˝µă
µÄşá×ř±ęłË2Ł¬×Ý×ř±ęłË4Ł¬±äµ˝µă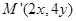 ˇŁ
ˇŁ
Ł¨1Ł©Çó±ä»»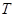 µÄľŘŐóŁ»
µÄľŘŐóŁ»
Ł¨2Ł©Ô˛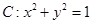 Ôڱ任
Ôڱ任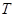 µÄ×÷ÓĂϱäłÉÁËʲôͼĐÎŁż
µÄ×÷ÓĂϱäłÉÁËʲôͼĐÎŁż
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁş¸ßÖĐĘýѧ Ŕ´Ô´Łş2012-2013ѧÄę˝ËŐʡÄĎͨĘĐşŁĂĹÖĐѧ¸ßČýŁ¨ÉĎŁ©żŞŃ§Ľě˛âĘýѧĘÔľíŁ¨˝âÎö°ćŁ© ĚâĐÍŁş˝â´đĚâ
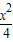 +
+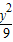 =1ÔÚM-1µÄ×÷ÓĂϵÄĐÂÇúĎߵķ˝łĚŁ®
=1ÔÚM-1µÄ×÷ÓĂϵÄĐÂÇúĎߵķ˝łĚŁ®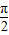 Ł©Ł¬ČôÖ±ĎßląýµăPŁ¬ÇŇÇăб˝ÇÎŞ
Ł©Ł¬ČôÖ±ĎßląýµăPŁ¬ÇŇÇăб˝ÇÎŞ 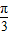 Ł¬Ô˛CŇÔMÎŞÔ˛Đġ˘4ÎŞ°ëľ¶Ł®
Ł¬Ô˛CŇÔMÎŞÔ˛Đġ˘4ÎŞ°ëľ¶Ł®˛éż´´đ°¸şÍ˝âÎö>>
ąúĽĘѧУÓĹѡ - Á·Ď°˛áÁбí - ĘÔĚâÁбí
şţ±±Ęˇ»ĄÁŞÍřÎĄ·¨şÍ˛»ÁĽĐĹϢľŮ±¨Ć˝Ě¨ | ÍřÉĎÓĐş¦ĐĹϢľŮ±¨×¨Çř | µçĐĹթƾٱ¨×¨Çř | ÉćŔúĘ·ĐéÎŢÖ÷ŇĺÓĐş¦ĐĹϢľŮ±¨×¨Çř | ÉćĆóÇÖȨľŮ±¨×¨Çř
ÎĄ·¨şÍ˛»ÁĽĐĹϢľŮ±¨µç»°Łş027-86699610 ľŮ±¨ÓĘĎ䣺58377363@163.com