
【题目】某公司试销某种“上海世博会”纪念品,每件按30元销售,可获利50%,设每件纪念品的成本为a元.
(1)试求a的值;
(2)公司在试销过程中进行了市场调查,发现销售量y(件)与每件售价x(元)满足关系y=-10x+800.设每天销售利润为W(元),求每天销售利润W(元)与每件售价x(元)之间的函数解析式;当每件售价为多少时,每天获得的利润最大?最大利润是多少?
【答案】(1) a=20;(2)详见解析.
【解析】试题分析:(1) 每件按30元销售,可获利50%,成本为a元,则a(1+50%)=30,解出a值即可;(2) 每天销售利润=销售量![]() (每件售价-成本) ,写出每天销售利润W(元)与每件售价x(元)之间的函数解析式,化简得到二次函数,用配方法求出最值.
(每件售价-成本) ,写出每天销售利润W(元)与每件售价x(元)之间的函数解析式,化简得到二次函数,用配方法求出最值.
试题解析:
(1)∵按30元销售,可获利50%,∴a(1+50%)=30,解得a=20.
(2)∵销售量y(件)与每件售价x(元)满足关系y=-10x+800,则每天销售利润W(元)与每件售价x(元)满足W=(-10x+800)(x-20)=-10x2+1 000x+16 000=-10(x-50)2+9 000,
故当x=50时,W取最大值9 000,
即每件售价为50元时,每天获得的利润最大,最大利润是9 000元.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]()
![]() (t+1)lnx,,其中t∈R.
(t+1)lnx,,其中t∈R.
(1)若t=1,求证:当x>1时,f(x)>0成立;
(2)若t>![]() ,判断函数g(x)=x[f(x)+t+1]的零点的个数.
,判断函数g(x)=x[f(x)+t+1]的零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两种商品,经营销售这两种商品所得的利润依次为M万元和N万元,它们与投入资金![]() 万元的关系可由经验公式给出:M=
万元的关系可由经验公式给出:M=![]() ,N=
,N=![]() (
(![]() ≥1).今有8万元资金投入经营甲、乙两种商品,且乙商品至少要求投资1万元,
≥1).今有8万元资金投入经营甲、乙两种商品,且乙商品至少要求投资1万元,
设投入乙种商品的资金为![]() 万元,总利润
万元,总利润![]() ;
;
(2)为获得最大利润,对甲、乙两种商品的资金投入分别是多少?共能获得多大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,沿
,沿![]() 将四边形
将四边形![]() 折起,连接
折起,连接![]() .
.
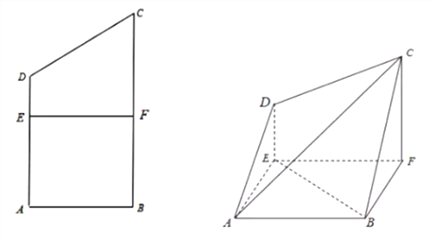
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() .
.
(I)求二面角![]() 的平面角的大小;
的平面角的大小;
(II)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·哈尔滨高二检测)如图,下列四个几何体中,它们的三视图(正视图、俯视图、侧视图)有且仅有两个相同,而另一个不同的两个几何体是________.


(1)棱长为2的正方体 (2)底面直径和高均为2的圆柱

(3)底面直径和高
均为2的圆锥
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
设椭圆![]() 的离心率为
的离心率为![]() ,其左焦点
,其左焦点![]() 与抛物线
与抛物线![]() 的焦点相同.
的焦点相同.
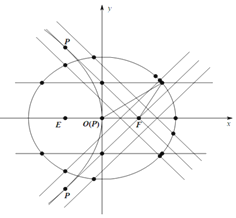
(1)求此椭圆的方程;
(2)若过此椭圆的右焦点![]() 的直线
的直线![]() 与曲线
与曲线![]() 只有一个交点
只有一个交点![]() ,则
,则
①求直线![]() 的方程;
的方程;
②椭圆上是否存在点![]() ,使得
,使得![]() ,若存在,请说明一共有几个点;若不存在,请说明理由.
,若存在,请说明一共有几个点;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() ,设函数
,设函数![]() .
.
(1)若函数![]() 的图象关于直线
的图象关于直线![]() 对称,且
对称,且![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)在(1)的条件下,当![]() 时,函数
时,函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com