【题目】制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损．某投资人打算投资甲、乙两个项目．根据预测，甲、乙项目可能的最大盈利率分别为100%和50%，可能的最大亏损分别为30%和10%．投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元．问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？
【答案】投资人用4万元投资甲项目、6万元投资乙项目，才能在确保亏损不超过1.8 万元的前提下，使可能的盈利最大
【解析】试题分析：(1)含有实际背景的线性规划问题其解题关键是找到制约求解目标的两个变量，用这两个变量建立可行域和目标函数，解题时要注意题目中的各种制约的关系，列出全面的制约条件和正确的目标函数；（2）平面区域的画法：线定界、点定线（注意实虚线）；(3)求最值：求二元一次函数
的最值，将函数转化为直线的点斜式
，通过求直线的截距
的最值间接求出
的最值，最优解在顶点或边界取得.
试题解析：解：设分别向甲、乙两组项目投资
万元，
万元，利润为万元
由题意知
目标函数
作出可行域
作出可行域
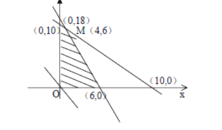
作直线
，并作平行直线
的一组直线
，与可行域相交，其中有一条直线经过可行域上的点
点，且与直线
的距离
最大，这里是直线
和
解方程组
，解得
此时
（万元）
当时最大
答:投资人投资甲项目4万元，乙项目6万元，获得利润最大
科目：高中数学 来源： 题型：
【题目】已知直线l、m，平面α、β，下列命题正确的是 ( )
A. l∥β，lαα∥β
B. l∥β，m∥β，lα，mαα∥β
C. l∥m，lα，mβα∥β
D. l∥β，m∥β，lα，mα，l∩m＝Mα∥β
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某理科考生参加自主招生面试，从7道题中（4道理科题3道文科题）不放回地依次任取3道作答.
（1）求该考生在第一次抽到理科题的条件下，第二次和第三次均抽到文科题的概率；
（2）规定理科考生需作答两道理科题和一道文科题，该考生答对理科题的概率均为
，答对文科题的概率均为
，若每题答对得10分，否则得零分.现该生已抽到三道题（两理一文），求其所得总分
的分布列与数学期望
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司试销某种“上海世博会”纪念品，每件按30元销售，可获利50%，设每件纪念品的成本为a元．
(1)试求a的值；
(2)公司在试销过程中进行了市场调查，发现销售量y(件)与每件售价x(元)满足关系y＝－10x＋800.设每天销售利润为W(元)，求每天销售利润W(元)与每件售价x(元)之间的函数解析式；当每件售价为多少时，每天获得的利润最大？最大利润是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【2017届广东省珠海市高三上学期期末考试文数】已知函数
的最小值为0，其中
，设
.
(1)求
的值；
(2)对任意
恒成立，求实数
的取值范围；
(3)讨论方程
在
上根的个数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【2014福建,文22】已知函数
（
为常数）的图像与
轴交于点
，曲线
在点
处的切线斜率为
.
（1）求
的值及函数
的极值；
（2）证明：当
时，
（3）证明：对任意给定的正数
，总存在
，使得当
时，恒有
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知二次函数
（其中
）满足下列3个条件:
①函数
的图象过坐标原点；
②函数的对称轴方程为
；
③方程
有两个相等的实数根，
令
.
（1）求函数
的解析式；
（2）求使不等式
恒成立的实数
的取值范围；
（3）已知函数
在
上的最小值为
，求实数
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
