
分析 利用平面中的射影定理证明;将平面中的三角形类比成空间的三棱锥,三角形的两边垂直类比成三棱锥的三棱垂直,得到类比性质通过作辅助线将空间的证明问题转化为三角形中的性质.
解答 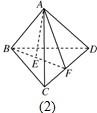 解:类比AB⊥AC,AD⊥BC猜想:在四面体ABCD中,若AB⊥AC,AB⊥AD,AC⊥AD,AE⊥平面BCD,则$\frac{1}{A{E}^{2}}$=$\frac{1}{A{D}^{2}}$+$\frac{1}{A{B}^{2}}$+$\frac{1}{A{C}^{2}}$.
解:类比AB⊥AC,AD⊥BC猜想:在四面体ABCD中,若AB⊥AC,AB⊥AD,AC⊥AD,AE⊥平面BCD,则$\frac{1}{A{E}^{2}}$=$\frac{1}{A{D}^{2}}$+$\frac{1}{A{B}^{2}}$+$\frac{1}{A{C}^{2}}$.
如图,连接BE交CD于F,连接AF.
∵AB⊥AC,AB⊥AD
∴AB⊥平面ACD.
而AF?平面ACD,∴AB⊥AF.
在Rt△ABF中,AE⊥BF,
∴$\frac{1}{A{E}^{2}}$=$\frac{1}{A{B}^{2}}$+$\frac{1}{A{F}^{2}}$
在Rt△ACD中,AF⊥CD,
∴$\frac{1}{A{F}^{2}}$=$\frac{1}{A{D}^{2}}$+$\frac{1}{A{C}^{2}}$,
∴$\frac{1}{A{E}^{2}}$=$\frac{1}{A{D}^{2}}$+$\frac{1}{A{B}^{2}}$+$\frac{1}{A{C}^{2}}$.
故猜想正确,
故答案为$\frac{1}{A{D}^{2}}$+$\frac{1}{A{B}^{2}}$+$\frac{1}{A{C}^{2}}$.
点评 本题考查利用类比推理得到结论、证明类比结论时证明过程与其类比对象的证明过程类似或直接转化为类比对象的结论.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:选择题
| A. | y=sin($\frac{x}{2}$-$\frac{π}{8}$) | B. | y=sin($\frac{x}{2}$+$\frac{π}{8}$) | C. | y=sin(2x-$\frac{π}{8}$) | D. | y=sin(2x-$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,D是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一个点 | B. | 两个点 | C. | 一条线段 | D. | 两条线段 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
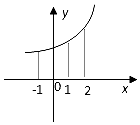 已知函数y=f(x)的图象如图所示,设函数y=f(x)从-1到1的平均变化率为v1,从1到2的平均变化率为v2,则v1与v2的大小关系为( )
已知函数y=f(x)的图象如图所示,设函数y=f(x)从-1到1的平均变化率为v1,从1到2的平均变化率为v2,则v1与v2的大小关系为( )| A. | v1>v2 | B. | v1=v2 | C. | v1<v2 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2)∪(2,+∞) | B. | (-∞,-2)∪(-2,+∞) | C. | (-∞,$\frac{5}{2}$)∪($\frac{5}{2}$,+∞) | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinA+sinB=0.2 | B. | $\overrightarrow{AB}$•$\overrightarrow{BC}$<0 | ||
| C. | b=3,c=3$\sqrt{3}$,B=30° | D. | tanA+tanB+tanC>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com