
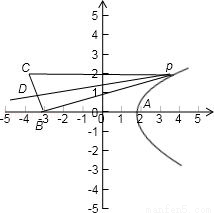
A、B、C是我方三个炮兵阵地,A在B正东6 km,C在B正北偏西30°,相距4 km,P为敌炮阵地,某时刻A处发现敌炮阵地的某种信号,由于B、C两地比A距P地远,因此4 s后,B、C才同时发现这一信号,此信号的传播速度为1 km/s,A若炮击P地,求炮击的方位角.
北偏东30°
【解析】
试题分析:建立坐标系,因为|PB|=|PC|,所以点P在线段BC的垂直平分线上,写出中垂线的方程,又|PB|﹣|PA|=4,故P在以A、B为焦点的双曲线右支上,写出双曲线方程,将这2个方程联立方程组,解出交点P的坐标,由PA斜率计算炮击的方位角.
【解析】
如图,以直线BA为x轴,线段BA的中垂线为y轴建立坐标系,则
B(﹣3,0)、A(3,0)、C(﹣5,2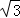 ).
).
因为|PB|=|PC|,所以点P在线段BC的垂直平分线上.
因为kBC=﹣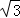 ,BC中点D(﹣4,
,BC中点D(﹣4,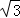 ),
),
所以直线PD的方程为y﹣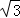 =
=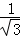 (x+4).①
(x+4).①
又|PB|﹣|PA|=4,故P在以A、B为焦点的双曲线右支上.
设P(x,y),则双曲线方程为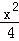 ﹣
﹣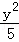 =1(x≥0).②
=1(x≥0).②
联立①②,得x=8,y=5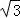 ,
,
所以P(8,5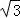 ).因此kPA=
).因此kPA=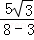 =
=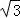 .
.
故炮击的方位角为北偏东30°.


科目:高中数学 来源:[同步]2014年苏教版必修一 1.2 子集、全集、补集练习卷(解析版) 题型:填空题
设x,y∈R,B={(x,y)|y﹣3=x﹣2},A={(x,y)|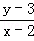 =1},则集合A与B的关系是 .
=1},则集合A与B的关系是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.1 导数的概念练习卷(解析版) 题型:解答题
已知函数f(x)=2x2+3,分别计算函数f(x)在下列区间上的平均变化率:
(1)[2,4];
(2)[2,3];
(3)[2,2.1];
(4)[2,2.001].
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷(解析版) 题型:解答题
某大桥在涨水时有最大跨度的中央桥孔如图所示,已知上部呈抛物线形,跨度为20 m,拱顶距水面6 m,桥墩高出水面4 m,现有一货船欲过此孔,该货船水下宽度不超过18 m,目前吃水线上部分中央船体高5 m,宽16 m,且该货船在现在状况下还可多装1000 t货物,但每多装150 t货物,船体吃水线就要上升0.04 m,若不考虑水下深度,该货船在现在状况下能否直接或设法通过该桥孔?为什么?
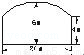
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷(解析版) 题型:填空题
(5分)一个酒杯的轴截面是抛物线的一部分,它的方程是x2=2y(0≤y≤20).在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围为
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.3 抛物线练习卷(解析版) 题型:选择题
以双曲线 =1的右顶点为焦点的抛物线的标准方程为( )
=1的右顶点为焦点的抛物线的标准方程为( )
A.y2=16x B.y2=﹣16x C.y2=8x D.y2=﹣8x
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修二 3.1 弧度制与任意角练习卷2(解析版) 题型:解答题
(8分)1弧度的圆心角所对的弦长为2,求这个圆心角所对的弧长及圆心角所夹的扇形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com