练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （5分）一个酒杯的轴截面是抛物线的一部分，它的方程是x2=2y（0≤y≤20）．在杯内放入一个玻璃球，要使球触及酒杯底部，则玻璃球的半径r的范围为

     

    0＜r≤1

    【解析】

    试题分析：设小球圆心（0，y0） 抛物线上点（x，y），求得点到圆心距离平方 的表达式，进而根据若r2最小值在（0，0）时取到，则小球触及杯底 需1﹣y0≥0 进而求得r的范围．

    【解析】
    设小球圆心（0，y0）

    抛物线上点（x，y）

    点到圆心距离平方

    r2=x2+（y﹣y0）2=2y+（y﹣y0）2=Y2+2（1﹣y0）y+y02

    若r2最小值在（0，0）时取到，则小球触及杯底

    所以1﹣y0≥0

    所以0＜y0≤1

    所以0＜r≤1

    故答案为0＜r≤1

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 3.4 生活中的优化问题举例练习卷（解析版） 题型：填空题

    某公司租地建仓库，每月土地占用费y1与仓库到车站的距离成反比，而每月库存货物的运费y2与到车站的距离成正比，如果在距离车站10千米处建仓库，这两项费用y1和y2分别为2万元和8万元，那么，要使这两项费用之和最小，仓库应建在离车站 千米处．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 3.2导数的运算练习卷（解析版） 题型：填空题

    若函数f（x）=ax4+bx2+c满足f′（1）=2，则f′（﹣1）= ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷（解析版） 题型：解答题

    A、B、C是我方三个炮兵阵地，A在B正东6 km，C在B正北偏西30°，相距4 km，P为敌炮阵地，某时刻A处发现敌炮阵地的某种信号，由于B、C两地比A距P地远，因此4 s后，B、C才同时发现这一信号，此信号的传播速度为1 km/s，A若炮击P地，求炮击的方位角．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷（解析版） 题型：解答题

    如图是一种加热水和食物的太阳灶，上面装有可旋转的抛物面形的反光镜，镜的轴截面是抛物线的一部分，盛水和食物的容器放在抛物线的焦点处，容器由若干根等长的铁筋焊接在一起的架子支撑．已知镜口圆的直径为12 m，镜深2 m，

    （1）建立适当的坐标系，求抛物线的方程和焦点的位置；

    （2）若把盛水和食物的容器近似地看作点，试求每根铁筋的长度．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷（解析版） 题型：选择题

    （4分）天安门广场，旗杆比华表高，在地面上，观察它们顶端的仰角都相等的各点所在的曲线是（ ）

    A.椭圆 B.圆 C.双曲线的一支 D.抛物线

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 2.3 抛物线练习卷（解析版） 题型：解答题

    根据下列条件写出抛物线的标准方程：

    （1）准线方程是y=3；

    （2）过点P（﹣2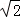，4）；

    （3）焦点到准线的距离为．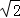

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版选修1-1 2.1 椭圆练习卷（解析版） 题型：选择题

    （3分）已知椭圆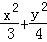=1的上焦点为F，直线x+y﹣1=0和x+y+1=0与椭圆分别相交于点A，B和C，D，则AF+BF+CF+DF=（ ）

    A.2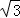 B.4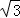 C.4 D.8

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年湘教版必修二 3.1 弧度制与任意角练习卷1（解析版） 题型：解答题

    （1）一个半径为r的扇形，若它的周长等于弧所在的半圆的长，那么扇形的圆心角是多少弧度？是多少度？扇形的面积是多少？

    （2）一扇形的周长为20 cm，当扇形的圆心角α等于多少弧度时，这个扇形的面积最大？

     

    查看答案和解析>>

    同步练习册答案