
(1)一个半径为r的扇形,若它的周长等于弧所在的半圆的长,那么扇形的圆心角是多少弧度?是多少度?扇形的面积是多少?
(2)一扇形的周长为20 cm,当扇形的圆心角α等于多少弧度时,这个扇形的面积最大?
(1)π﹣2,65°26′, (π﹣2)r2.
(π﹣2)r2.
(2)当α=2rad时,扇形的面积取最大值.
【解析】
试题分析:(1)设扇形的圆心角,利用弧长公式得到弧长,代入题中条件,求出圆心角的弧度数,再化为度数,利用扇形的面积公式求扇形的面积.
(2)设出弧长和半径,由周长得到弧长和半径的关系,再把弧长和半径的关系代入扇形的面积公式,转化为关于半径的二次函数,配方求出面积的最大值.
【解析】
(1)设扇形的圆心角是θrad,因为扇形的弧长是rθ,
所以扇形的周长是2r+rθ.依题意,得2r+rθ=πr,
∴θ=π﹣2=(π﹣2)×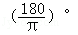 ≈1.142×57.30°≈65.44°≈65°26′,
≈1.142×57.30°≈65.44°≈65°26′,
∴扇形的面积为S= r2θ=
r2θ= (π﹣2)r2.
(π﹣2)r2.
(2)设扇形的半径为r,弧长为l,则l+2r=20,
即l=20﹣2r(0<r<10)①
扇形的面积S= lr,将①代入,得S=
lr,将①代入,得S= (20﹣2r)r=﹣r2+10r=﹣(r﹣5)2+25,
(20﹣2r)r=﹣r2+10r=﹣(r﹣5)2+25,
所以当且仅当r=5时,S有最大值25.此时
l=20﹣2×5=10,α= =2.所以当α=2rad时,扇形的面积取最大值.
=2.所以当α=2rad时,扇形的面积取最大值.



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷(解析版) 题型:填空题
(5分)一个酒杯的轴截面是抛物线的一部分,它的方程是x2=2y(0≤y≤20).在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围为
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.1 椭圆练习卷(解析版) 题型:选择题
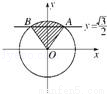
(3分)已知椭圆C的左、右焦点坐标分别是(﹣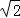 ,0),(
,0),(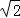 ,0),离心率是
,0),离心率是 ,则椭圆C的方程为( )
,则椭圆C的方程为( )
A.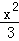 +y2=1 B.x2+
+y2=1 B.x2+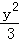 =1 C.
=1 C.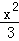 +y
+y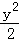 =1 D.
=1 D.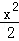 +
+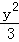 =1
=1
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修二 3.1 弧度制与任意角练习卷2(解析版) 题型:解答题
(8分)1弧度的圆心角所对的弦长为2,求这个圆心角所对的弧长及圆心角所夹的扇形的面积.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修二 3.1 弧度制与任意角练习卷2(解析版) 题型:选择题
(2分)将分针拨快10分钟,则分针转过的弧度数是( )
A.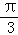 B.﹣
B.﹣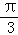 C.
C. D.﹣
D.﹣
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修三 7.5 空间直角坐标系练习卷(解析版) 题型:
在空间直角坐标系O﹣xyz中,z=1的所有点构成的图形是 .点P(2,3,5)到平面xOy的距离为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.3平均值不等式练习卷(解析版) 题型:选择题
已知x,y,z∈R,且x+y+z=8,x2+y2+z2=24,则x的取值范围是( )
A.[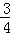 ,4] B.[
,4] B.[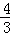 ,4] C.[
,4] C.[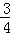 ,3] D.[
,3] D.[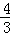 ,3]
,3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com