
根据下列条件写出抛物线的标准方程:
(1)准线方程是y=3;
(2)过点P(﹣2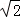 ,4);
,4);
(3)焦点到准线的距离为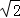 .
.
(1)x2=﹣12y.
(2)y2=﹣4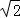 x或x2=2y.
x或x2=2y.
(3)y2=2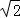 x,y2=﹣2
x,y2=﹣2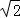 x,x2=2
x,x2=2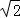 y或x2=﹣2
y或x2=﹣2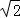 y.
y.
【解析】
试题分析:利用抛物线的定义及其性质即可得出.
解 (1)由准线方程为y=3知抛物线的焦点在y轴负半轴上,且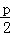 =3,则p=6,故所求抛物线的标准方程为x2=﹣12y.
=3,则p=6,故所求抛物线的标准方程为x2=﹣12y.
(2)∵点P(﹣2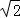 ,4)在第二象限,
,4)在第二象限,
∴设所求抛物线的标准方程为y2=﹣2px(p>0)或x2=2py(p>0),
将点P(﹣2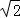 ,4)代入y2=﹣2px,得p=2
,4)代入y2=﹣2px,得p=2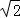 ;代入x2=2py,得p=1.
;代入x2=2py,得p=1.
∴所求抛物线的标准方程为y2=﹣4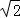 x或x2=2y.
x或x2=2y.
(3)由焦点到准线的距离为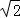 ,得p=
,得p=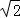 ,
,
故所求抛物线的标准方程为y2=2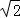 x,y2=﹣2
x,y2=﹣2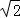 x,x2=2
x,x2=2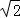 y或x2=﹣2
y或x2=﹣2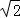 y.
y.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014年湘教版选修1-1 3.3导数在研究函数中的应用练习卷(解析版) 题型:解答题
(2014•上海二模)已知:函数f(x)=x3﹣6x+5,x∈R,
(1)求:函数f(x)的单调区间和极值;
(2)若关于x的方程f(x)=a有3个不同实根,求:实数a的取值范围;
(3)当x∈(1,+∞)时,f(x)≥k(x﹣1)恒成立,求:实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷(解析版) 题型:填空题
(5分)一个酒杯的轴截面是抛物线的一部分,它的方程是x2=2y(0≤y≤20).在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r的范围为
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.4 圆锥曲线的应用练习卷(解析版) 题型:选择题
(4分)一抛物线型拱桥,当水面离桥顶2m时,水面宽4m,若水面下降1m时,则水面宽为( )
A.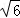 m B.2
m B.2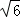 m C.4.5m D.9m
m C.4.5m D.9m
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.3 抛物线练习卷(解析版) 题型:选择题
以双曲线 =1的右顶点为焦点的抛物线的标准方程为( )
=1的右顶点为焦点的抛物线的标准方程为( )
A.y2=16x B.y2=﹣16x C.y2=8x D.y2=﹣8x
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.1 椭圆练习卷(解析版) 题型:选择题
(3分)(2014•成都一模)已知椭圆C: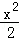 +y2=1的右焦点为F,右准线为l,点A∈l,线段AF交C于点B,若
+y2=1的右焦点为F,右准线为l,点A∈l,线段AF交C于点B,若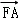 =3
=3 ,则|
,则|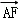 |=( )
|=( )
A.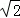 B.2 C.
B.2 C.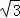 D.3
D.3
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.1 椭圆练习卷(解析版) 题型:选择题
(3分)已知椭圆C的左、右焦点坐标分别是(﹣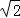 ,0),(
,0),(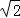 ,0),离心率是
,0),离心率是 ,则椭圆C的方程为( )
,则椭圆C的方程为( )
A.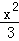 +y2=1 B.x2+
+y2=1 B.x2+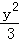 =1 C.
=1 C.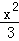 +y
+y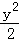 =1 D.
=1 D.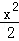 +
+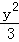 =1
=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com