
����Ŀ��ijͶ�ʹ�˾���ṩ����һ����Ͷ�����Ʒ�����һ���Ͷ��ӯ����������±���
Ͷ�ʹ��� | ���� | ���ⲻ | ���� | ������� | ���� | ���ⲻ | ���� | |
���� |
|
|
| ���� |
|
|
|
���ס���������Ͷ�ʹ��ʵĽ����·ֱ�ѡ��Ͷ�ʹ��С��͡�����𡱣���һ���������������һ��ӯ���ĸ��ʴ���![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ��ij������
��ij������![]() ��Ԫ�ʽ𣬾����ڡ�Ͷ�ʹ��С��͡�������������ַ�����ѡ���һ�֣���ôѡ����ַ�����ʹ��һ����Ͷ���������ѧ����ֵ�ϴ�.
��Ԫ�ʽ𣬾����ڡ�Ͷ�ʹ��С��͡�������������ַ�����ѡ���һ�֣���ôѡ����ַ�����ʹ��һ����Ͷ���������ѧ����ֵ�ϴ�.
���𰸡�����![]() ����Ӧѡ��Ͷ�ʹ��С���ʹ��һ����Ͷ���������ѧ����ֵ�ϴ�
����Ӧѡ��Ͷ�ʹ��С���ʹ��һ����Ͷ���������ѧ����ֵ�ϴ�
������������������� I�����¼�![]() Ϊ����Ͷ�ʹ�����ӯ�������¼�
Ϊ����Ͷ�ʹ�����ӯ�������¼�![]() Ϊ���ҹ��������ӯ�������¼�
Ϊ���ҹ��������ӯ�������¼�![]() Ϊ��һ���ס�����������һ��ӯ��������
Ϊ��һ���ס�����������һ��ӯ��������![]() ������A��B�����������������¼��������¼��ĸ��ʼ��㹫ʽ���ɵó����ʣ�
������A��B�����������������¼��������¼��ĸ��ʼ��㹫ʽ���ɵó����ʣ�
�� II���������ѡ��Ͷ�ʹ��С����Ǧ�Ϊӯ������λ��Ԫ�����ɵæεķֲ���Ϊ���������ѡ������𡱣��Ǧ�Ϊӯ������λ��Ԫ�����ɵæǵķֲ��У����㼴�ɱȽϳ���С��ϵ��
���������
�������¼�![]() Ϊ����Ͷ�ʹ�����ӯ�������¼�
Ϊ����Ͷ�ʹ�����ӯ�������¼�![]() Ϊ���ҹ��������ӯ�������¼�
Ϊ���ҹ��������ӯ�������¼�![]() Ϊ��һ���ס�����������һ��ӯ��������
Ϊ��һ���ס�����������һ��ӯ��������![]() ������
������![]() �������
�������
��Ϊ![]() ����
����![]() ����
����
![]() ,��
,��![]() ���
���![]() ��
��
����Ϊ![]() ��
��![]() ������
������![]() ����
����![]() ��
��
���������ѡ��Ͷ�ʹ��С�����![]() Ϊӯ������λ��Ԫ������
Ϊӯ������λ��Ԫ������![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��

��![]()
�������ѡ������𡱣���![]() Ϊӯ������λ��Ԫ������
Ϊӯ������λ��Ԫ������![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��

��![]()
��Ϊ![]() ����
����![]() ������Ӧѡ��Ͷ�ʹ��С���ʹ��һ����Ͷ���������ѧ����ֵ�ϴ�.
������Ӧѡ��Ͷ�ʹ��С���ʹ��һ����Ͷ���������ѧ����ֵ�ϴ�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������еĺ���f��x����g��x����ȣ� ��
A.f��x��=x2 �� ![]()
B.f��x��=x+1��g��x��= ![]() +1
+1
C.f��x��=x��g��x��= ![]()
D.f��x��= ![]() ��g��x��=
��g��x��= ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ��ˮƽ���õij�������ľ�İ�ȫ���������ĺ��d��ƽ���Ϳ���a�ij˻������ȣ������ij���l��ƽ���ɷ��ȣ� 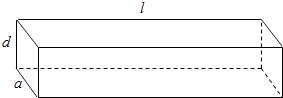
��1����a��d��0�������£�������ľ��ת90�㣨�����ȱ�Ϊ�˺�ȣ�����ľ�İ�ȫ���ɻᷢ���仯�𣿱���DZ�С��
��2������һ�������Ϊ��Բ����Բ�İ뾶ΪR= ![]() ��������ľ�ģ�������ȡ�ɺ����Ϊ�����ε���ľ���䳤�ȼ�Ϊ��ľ�涨�ij���l���ʺ������ν�ȡ����ʹ��ȫ�������
��������ľ�ģ�������ȡ�ɺ����Ϊ�����ε���ľ���䳤�ȼ�Ϊ��ľ�涨�ij���l���ʺ������ν�ȡ����ʹ��ȫ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ָ��ҵ��У������վ�㡢����վ�㡢����������ҵ�����������������ṩ���г��������������ǹ������õ�һ������̬��һ������������ҵ��ij�����о͡�һ����һ��������ƽ���ɱ�����λ��Ԫ�������õ�������������λ��������֮��Ĺ�ϵ�����е����о����ڵ�������н�����ͳ�ƣ��ó�������ݼ��±���
���õ������� | 2 | 3 | 4 | 5 | 8 |
ÿ��һ����ƽ���ɱ� | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
�����������ݣ��о���Ա�ֱ�����ס������ֲ�ͬ�Ļع�ģ�ͣ��õ������ع鷽�̣����̼ף� ![]() �������ң�
�������ң� ![]() .
.
��1��Ϊ����������ģ�͵����Ч���������������
������±�����������ȷ��0.1������ע�� ![]() ��
�� ![]() ��Ϊ��Ӧ�ڵ�
��Ϊ��Ӧ�ڵ�![]() �IJвҲ�����������
�IJвҲ�����������
���õ������� | 2 | 3 | 4 | 5 | 8 | |
ÿ��һ����ƽ���ɱ� | 3.2 | 2 | 1.9 | 1.7 | ||
ģ�ͼ� | ����ֵ | 2.4 | 2.1 | 1.6 | ||
�в� | 0 |
| 0.1 | |||
ģ���� | ����ֵ | 2.3 | 2 | 1.9 | ||
�в� | 0.1 | 0 | 0 | |||
�ڷֱ����ģ�ͼ���ģ���ҵIJв�ƽ����![]() ��
��![]() ����ͨ���Ƚ�
����ͨ���Ƚ�![]() ��
�� ![]() �Ĵ�С���ж��ĸ�ģ�����Ч������.
�Ĵ�С���ж��ĸ�ģ�����Ч������.
��2�������˾�ڸó���Ͷ�Ź����������ܵ������������һ�ӭ������������������Ӧ�����Ǹù�˾�о��Ƿ�����Ͷ�ţ������г����飬�������Ͷ��8ǧ��ʱ���ù�˾ƽ��һ����һ��������10Ԫ��6Ԫ����ĸ��ʷֱ�Ϊ0.6��0.4��Ͷ��1����ʱ���ù�˾ƽ��һ������һ��������10Ԫ��6Ԫ����ĸ��ʷֱ�Ϊ0.4��0.6���ʸù�˾Ӧ��Ͷ��8ǧ������1�����ܻ�ø�����������1�������Ч���Ϻõ�ģ�ͼ���һ����һ��������ƽ���ɱ����������롪�ɱ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x��=aex+ ![]() +b��a��0����
+b��a��0����
��1����f��x����[0��+�ޣ��ϵ���Сֵ��
��2��������y=f��x���ڵ㣨2��f��2���������߷���Ϊ3x��2y=0����a��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ʵ����R�ϵĿɵ�����f��x��������f��x+2�����溯������ ![]() ��2����ʽf��x����
��2����ʽf��x���� ![]() x��1�Ľ⼯�ǣ� ��
x��1�Ľ⼯�ǣ� ��
A.�����ޣ�2��
B.��2��+�ޣ�
C.��0��2��
D.�����ޣ�1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������p������x�IJ���ʽx2+��a��1��x+a2��0�Ľ⼯�ǿռ�������q����֪���κ���f��x��=x2��mx+2���� ![]() ���ҵ�x��[0��a]ʱ�����ֵ��2�������⡰p��q��Ϊ�٣���p��q��Ϊ�棬��ʵ��a��ȡֵ��Χ��
���ҵ�x��[0��a]ʱ�����ֵ��2�������⡰p��q��Ϊ�٣���p��q��Ϊ�棬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��֪Բ![]() ����
���� ![]() ��
��![]() ���㣬��Բ��C��ֱ��
���㣬��Բ��C��ֱ�� ![]() �ϣ���⣺��1��ԲC�ķ��̣���2����ֱ��
�ϣ���⣺��1��ԲC�ķ��̣���2����ֱ�� ![]() ��Բ
��Բ ![]() ���й����㣬��ʵ��
���й����㣬��ʵ�� ![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��1����ԲC�ķ��̣�
��2����ֱ�� ![]() ��Բ
��Բ ![]() ���й����㣬��ʵ��
���й����㣬��ʵ�� ![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com