
����Ŀ����ͼ��ʾ��һ��ˮƽ���õij�������ľ�İ�ȫ���������ĺ��d��ƽ���Ϳ���a�ij˻������ȣ������ij���l��ƽ���ɷ��ȣ� 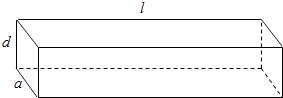
��1����a��d��0�������£�������ľ��ת90�㣨�����ȱ�Ϊ�˺�ȣ�����ľ�İ�ȫ���ɻᷢ���仯�𣿱���DZ�С��
��2������һ�������Ϊ��Բ����Բ�İ뾶ΪR= ![]() ��������ľ�ģ�������ȡ�ɺ����Ϊ�����ε���ľ���䳤�ȼ�Ϊ��ľ�涨�ij���l���ʺ������ν�ȡ����ʹ��ȫ�������
��������ľ�ģ�������ȡ�ɺ����Ϊ�����ε���ľ���䳤�ȼ�Ϊ��ľ�涨�ij���l���ʺ������ν�ȡ����ʹ��ȫ�������
���𰸡�
��1���⣺�谲ȫ����Ϊ ![]()
��ת90��� ![]() ��
��
�ɵã� ![]() ��
��
��a��d��0ʱ�� ![]() ��1
��1
��ʱ��ľ�İ�ȫ���ɱ��
��2���⣺���ȡ�Ŀ�Ϊa��0��a��2 ![]() ������Ϊd��
������Ϊd�� ![]() ����a2+d2=12
����a2+d2=12
�䳤��l��kΪ��ֵ����ȫ����Ϊ ![]()
�� ![]() ��
�� ![]()
��ʱ ![]()
��g�䣨a����0���ɵ� ![]() ��
��
�� ![]()
���Ե���a=2ʱ��g��a��ȡ��ȡ��ֵ����ʱ�� ![]() ��
��
���ԣ�����a=2���� ![]() ʱ����ȫ�������
ʱ����ȫ�������
����������1���谲ȫ����Ϊ ![]() �������ת90���ı���ʽ��Ȼ������ֵ�����ֵ����2�����ȡ�Ŀ�Ϊa��0��a��2
�������ת90���ı���ʽ��Ȼ������ֵ�����ֵ����2�����ȡ�Ŀ�Ϊa��0��a��2 ![]() ������Ϊd��
������Ϊd�� ![]() ���õ���ȫ����Ϊ
���õ���ȫ����Ϊ ![]()
�� ![]() ��
�� ![]() ���ú����ĵ���������ֵ���ɣ�
���ú����ĵ���������ֵ���ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=loga ![]() ����a��0��a��1����
����a��0��a��1����
��1���ж�f��x������ż�ԣ�������֤����
��2���Ƿ����ʵ��mʹ��f��x+2��+f��m��x��Ϊ�����������ڣ����m��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������D�ϵĺ���f��x����ͬʱ���㣺�ٴ���M��0��ʹ�ö������x1 �� x2��D������|f��x1����f��x2��|��M����f��x����ͼ����ڶԳ����ģ����f��x��Ϊ��P����������
��֪����f1��x��= ![]() ��f2��x��=lg��
��f2��x��=lg�� ![]() ��x���������½���һ����ȷ���ǣ� ��
��x���������½���һ����ȷ���ǣ� ��
A.f1��x���� f2��x������P������
B.f1��x����P��������f2��x������P������
C.f1��x������P��������f2��x����P������
D.f1��x���� f2��x��������P������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
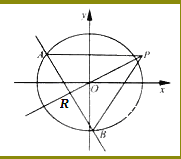
����Ŀ����ͼ����ԲC�� ![]() (a��b��0)��������Ϊ
(a��b��0)��������Ϊ![]() �����㵽��
�����㵽��![]() �ľ���Ϊ
�ľ���Ϊ![]() ������ԭ��O��ֱ��
������ԭ��O��ֱ��![]() ��C�ཻ��A��B���㣬���߶�AB��ֱ��OPƽ�֣�
��C�ཻ��A��B���㣬���߶�AB��ֱ��OPƽ�֣�
��1������ԲC�ķ��̣�
��2����![]() ABP�����ȡ���ʱֱ��l�ķ��̣�
ABP�����ȡ���ʱֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ΪR�ĺ���f��x��= ![]() ���溯����
���溯����
��1����a��b��ֵ��
��2���жϺ���f��x���ĵ����ԣ����ö���֤����
��3������������ ![]() ����f��kx2��+f��2x��1����0��������ʵ��k��ȡֵ��Χ��
����f��kx2��+f��2x��1����0��������ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=x2+bx��alnx��
��1����x=2�Ǻ���f��x���ļ�ֵ�㣬1��x0�Ǻ���f��x����������ͬ��㣬��x0�ʣ�n��n+1����n��N����n��
��2����������b��[��2����1]��������x�ʣ�1��e����eΪ��Ȼ�����ĵ�������ʹ��f��x����0��������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��У��һ���6�ڿ�������������ġ���ѧ�����������Ļ��κ��������������θ�1�ڣ����ڿγ̱��ϵ����������Ļ���֮�������1�������εĸ���Ϊ�����������𣩣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͶ�ʹ�˾���ṩ����һ����Ͷ�����Ʒ�����һ���Ͷ��ӯ����������±���
Ͷ�ʹ��� | ���� | ���ⲻ | ���� | ������� | ���� | ���ⲻ | ���� | |
���� |
|
|
| ���� |
|
|
|
���ס���������Ͷ�ʹ��ʵĽ����·ֱ�ѡ��Ͷ�ʹ��С��͡�����𡱣���һ���������������һ��ӯ���ĸ��ʴ���![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ��ij������
��ij������![]() ��Ԫ�ʽ𣬾����ڡ�Ͷ�ʹ��С��͡�������������ַ�����ѡ���һ�֣���ôѡ����ַ�����ʹ��һ����Ͷ���������ѧ����ֵ�ϴ�.
��Ԫ�ʽ𣬾����ڡ�Ͷ�ʹ��С��͡�������������ַ�����ѡ���һ�֣���ôѡ����ַ�����ʹ��һ����Ͷ���������ѧ����ֵ�ϴ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��̨�����Ĵ�A����ÿСʱ20ǧ���ٶ�������ƫ��![]() ���ƶ�����̨�����IJ�����300ǧ�ĵ���ΪΣ������.����B��A�ص�����400ǧ�״�.�뽨��ǡ����ƽ��ֱ������ϵ������������⣺
���ƶ�����̨�����IJ�����300ǧ�ĵ���ΪΣ������.����B��A�ص�����400ǧ�״�.�뽨��ǡ����ƽ��ֱ������ϵ������������⣺

(1) ��̨���ƶ�·�����ڵ�ֱ�߷���;
(2)�����B����Σ�������ʱ���Ƕ���Сʱ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com