
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,且过点(1,
,且过点(1,![]() ).
).
(I)求椭圆C的方程;
(Ⅱ)设与圆O:x2+y2=![]() 相切的直线l交椭圆C与A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程.
相切的直线l交椭圆C与A,B两点,求△OAB面积的最大值,及取得最大值时直线l的方程.
【答案】(I)![]() (Ⅱ)△OAB面积的最大值为
(Ⅱ)△OAB面积的最大值为![]() ,此时直线方程
,此时直线方程![]()
【解析】
试题分析:(1)运用椭圆的离心率公式和点满足椭圆方程,解方程可得a,b,进而得到椭圆方程;(2)讨论①当k不存在时,②当k存在时,设直线为y=kx+m,A![]() ,B
,B![]() ,将直线y=kx+m代入椭圆方程,运用韦达定理和弦长公式,以及直线和圆相切的条件:d=r,结合基本不等式即可得到所求面积的最大值和直线l的方程
,将直线y=kx+m代入椭圆方程,运用韦达定理和弦长公式,以及直线和圆相切的条件:d=r,结合基本不等式即可得到所求面积的最大值和直线l的方程
试题解析:(1)由题意可得,e=![]() =
=![]() ,a2﹣b2=c2,点(1,
,a2﹣b2=c2,点(1,![]() )代入椭圆方程,可得
)代入椭圆方程,可得
![]() +
+![]() =1,解得a=
=1,解得a=![]() ,b=1,即有椭圆的方程为
,b=1,即有椭圆的方程为![]() ;
;
(2)①当k不存在时,x=±![]() 时,可得y=±
时,可得y=±![]() ,S△OAB=
,S△OAB=![]() ×
×![]() ×
×![]() =
=![]() ;
;
②当k存在时,设直线为y=kx+m,A(x1,y1),B(x2,y2),
将直线y=kx+m代入椭圆方程可得(1+3k2)x2+6kmx+3m2﹣3=0,
x1+x2=﹣![]() ,x1x2=
,x1x2=![]() ,
,
由直线l与圆O:x2+y2=![]() 相切,可得
相切,可得![]() =
=![]() ,即有4m2=3(1+k2),
,即有4m2=3(1+k2),
|AB|=![]()
![]() =
=![]()
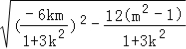
=![]()
![]() =
=![]()
![]()
=![]()
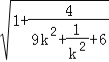 ≤
≤![]()
![]() =2,
=2,
当且仅当9k2=![]() 即k=±
即k=±![]() 时等号成立,可得S△OAB=
时等号成立,可得S△OAB=![]() |AB|r≤
|AB|r≤![]() ×2×
×2×![]() =
=![]() ,
,
即有△OAB面积的最大值为![]() ,此时直线方程y=±
,此时直线方程y=±![]() x±1.
x±1.


科目:高中数学 来源: 题型:
【题目】给出定义在![]() 上的两个函数
上的两个函数![]() ,
,![]() .
.
(1)若![]() 在
在![]() 处取最值.求
处取最值.求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上单调递减,求实数
上单调递减,求实数![]() 的取值范围;
的取值范围;
(3)试确定函数![]() 的零点个数,并说明理由.
的零点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c,若c=2![]() ,sinB=2sinA.
,sinB=2sinA.
(1)若C=![]() ,求a,b的值;
,求a,b的值;
(2)若cosC=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若<<0,则下列不等式:①<;②|a|+b>0;③a->b-;④lna2>lnb2中,正确的是( )
(A)①④ (B)②③ (C)①③ (D)②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】pH值是水溶液的重要理化参数。若溶液中氢离子的浓度为[H![]() ](单位:mol/l),则其pH值为-lg[H
](单位:mol/l),则其pH值为-lg[H![]() ]。在标准温度和气压下,若水溶液pH=7,则溶液为中性,pH<7时为酸性,pH>7时为碱性。例如,甲溶液中氢离子浓度为0.0001mol/l,其pH为-1g 0.0001,即pH=4。已知乙溶液的pH=2,则乙溶液中氢离子浓度为______mol/l。若乙溶液中氢离子浓度是丙溶液的两千万倍,则丙溶液的酸碱性为______(填中性、酸性或碱性)。
]。在标准温度和气压下,若水溶液pH=7,则溶液为中性,pH<7时为酸性,pH>7时为碱性。例如,甲溶液中氢离子浓度为0.0001mol/l,其pH为-1g 0.0001,即pH=4。已知乙溶液的pH=2,则乙溶液中氢离子浓度为______mol/l。若乙溶液中氢离子浓度是丙溶液的两千万倍,则丙溶液的酸碱性为______(填中性、酸性或碱性)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共100个,生产一个卫兵需5分钟,生产一个骑兵需7分钟,生产一个伞兵需4分钟,已知总生产时间不超过10小时,若生产一个卫兵可获利润5元,生产一个骑兵可获利润6元,生产一个伞兵可获利润3元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com