
分析 (1)求出f′(x),得到f′($\frac{1}{2}$)=0,解出a,利用导数的正负,即可求f(x)的单调区间;
(2)由于a≤1,所以ln(2x+a)≤ln(2x+1),所以f(x)≤ln(2x+1)-e2x-1,利用对任意x$>-\frac{1}{2}$,ln(2x+1)-e2x-1<0,即可求得a的取值范围.
解答 解:(1)f′(x)=$\frac{2}{2x+a}$-2e2x-1,由已知得 f′($\frac{1}{2}$)=0,即:$\frac{1}{1+a}$-1=0,
所以a=0,…(1分)
所以f(x)=ln2x-e2x-1,函数f(x)的定义域为(0,+∞),f′(x)=$\frac{1}{x}$-2e2x-1,…(2分)
由于f′(x) 在(0,+∞)上为减函数,而f′($\frac{1}{2}$)=0,所以当x∈(0,$\frac{1}{2}$)时,f′(x)>0;
当x∈($\frac{1}{2}$,+∞)时,f′(x)<0,
所以f(x)的单调递增区间为(0,$\frac{1}{2}$),单调递减区间为($\frac{1}{2}$,+∞).(5分)
(2)由于a≤1,所以ln(2x+a)≤ln(2x+1),所以f(x)≤ln(2x+1)-e2x-1,…(6分)
令g(x)=ln(2x+1)-2x(x>-$\frac{1}{2}$),则g′(x)=$\frac{-4x}{2x+1}$,
所以,当-$\frac{1}{2}$<x<0时,g′(x)>0,当x>0时,g′(x)<0,
所以g(x)≤g(0)=0,即:ln(2x+1)≤2x …(8分)
令h(x)=e2x-1-2x,则h′(x)=2( e2x-1-1),
所以,当x$>\frac{1}{2}$时,h′(x)>0,当-$\frac{1}{2}<x<\frac{1}{2}$时,h′(x)<0,
所以h(x)≥h($\frac{1}{2}$),即:e2x-1≥2x.…(10分)
所以,对任意x$>-\frac{1}{2}$,ln(2x+1)-e2x-1<0,
因此,当a≤1时,对任意x>-$\frac{a}{2}$,ln(2x+1)-e2x-1<0,所以x的取值范围为(-$\frac{a}{2}$,+∞) …(12分)
点评 本题考查了函数的单调性,考查导数知识的综合运用,考查学生转化问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
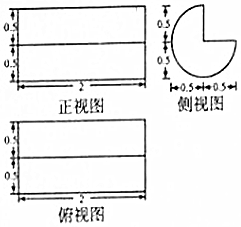 某同学在运动场所发现一实心椅子,其三视图如图所示(俯视图是圆的一部分及该圆的两条互相垂直的半径,有关尺寸如图,单位:m),经了解,建造该类椅子的平均成本为240元/m3,那么该椅子的建造成本约为(π≈3.14)( )
某同学在运动场所发现一实心椅子,其三视图如图所示(俯视图是圆的一部分及该圆的两条互相垂直的半径,有关尺寸如图,单位:m),经了解,建造该类椅子的平均成本为240元/m3,那么该椅子的建造成本约为(π≈3.14)( )| A. | 94.20元 | B. | 240.00元 | C. | 282.60元 | D. | 376.80元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
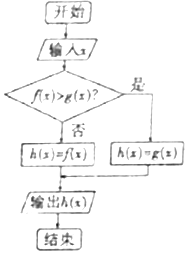
| A. | 2016 | B. | 2017 | C. | loga2016 | D. | loga2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com