
分析 (1)当a=1 时,f(x)=-x2+x+b,则f(x) 在[1,2]上单调递减,即可求M(1,b)关于b的解析式;
(2)函数y=f(x)的对称轴为$x=\frac{a}{2}$,下面讨论$\frac{a}{2},1,2$的大小关系来确定f(x)的单调性.利用对任意的a,b∈R,恒有M(a,b)≥M(a0,b0),求满足条件的所有实数对(a0,b0).
解答 解:(1)当a=1 时,f(x)=-x2+x+b,则f(x) 在[1,2]上单调递减,
故f(x) 在[1,2]上的值域为[b-2,b],
从而$M(a,b)=max\{|b-2|,|b|\}=\left\{\begin{array}{l}|b-2|,b≤1\\|b|,b>1\end{array}\right.$;
(2)函数y=f(x)的对称轴为$x=\frac{a}{2}$,
下面讨论$\frac{a}{2},1,2$的大小关系来确定f(x)的单调性.
①当a≤2或a≥4时,f(x)在[1,2]上单调,
又f(1)=a+b-1,f(2)=2a+b-4,M(a,b)=max{|a+b-1|,|2a+b-4|}
≥$\frac{1}{2}$(|a+b-1|+|2a+b-4|)≥$\frac{1}{2}$|a-3|≥$\frac{1}{2}$,
不等号1,2,3取到等号的条件分别为$\left\{\begin{array}{l}|2a+b-4|=|a+b-1|\\(2a+b-4)(a+b-1)<0\\ a=2\end{array}\right.$或$\left\{\begin{array}{l}|2a+b-4|=|a+b-1|\\(2a+b-4)(a+b-1)<0\\ a=4\end{array}\right.$,
从而$\left\{\begin{array}{l}a=2\\ b=-\frac{1}{2}\end{array}\right.$或$\left\{\begin{array}{l}a=4\\ b=-\frac{7}{2}\end{array}\right.$;
②当2<a<4时,f(x)在$[1,\frac{a}{2}]$上单调递增,在$[\frac{a}{2},2]$上单调递减,
又f(1)=a+b-1,f(2)=2a+b-4,$f(\frac{a}{2})=\frac{a^2}{4}+b$
ⅰ)当2<a≤3时,M(a,b)=max{|$\frac{{a}^{2}}{4}$+b|,|2a+b-4|}≥$\frac{1}{2}$(|$\frac{{a}^{2}}{4}$+b|+|2a+b-4|)≥$\frac{1}{2}$|$\frac{{a}^{2}}{4}$-2a+4|≥$\frac{1}{8}$
不等号1,2,3取到等号的条件分别为$\left\{\begin{array}{l}|\frac{a^2}{4}+b|=|2a+b-4|\\(\frac{a^2}{4}+b)(2a+b-4)<0\\ a=3\end{array}\right.$,故$\left\{\begin{array}{l}a=3\\ b=-\frac{17}{8}\end{array}\right.$.
ⅱ)当3<a≤4时,M(a,b)=max{|$\frac{{a}^{2}}{4}$+b|,|a+b--|}≥$\frac{1}{2}$(|$\frac{{a}^{2}}{4}$+b|+|a+b-1|)≥$\frac{1}{2}$|$\frac{{a}^{2}}{4}$-a+1|≥$\frac{1}{8}$
不等号1,2,3取到等号的条件分别为$\left\{\begin{array}{l}|\frac{a^2}{4}+b|=|a+b-1|\\(\frac{a^2}{4}+b)(a+b-1)<0\\ a=3\end{array}\right.$,
故$\left\{\begin{array}{l}a=3\\ b=-\frac{17}{8}\end{array}\right.$,这与3<a≤4矛盾.
综上所述,当且仅当a0=3,${b_0}=-\frac{17}{8}$时,对任意的a,b∈R,恒有$M(a,b)≥M({a_0},{b_0})=\frac{1}{8}$,故满足条件的所有实数对(a0,b0)为$(3,-\frac{17}{8})$.
点评 本题考查二次函数的性质,考查分类讨论的数学思想,考查学生的计算能力,难度大.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | $\frac{8\sqrt{14}}{7}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p>1 | B. | p≥1 | C. | p<1 | D. | p≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2π,2017π) | B. | (2π,2018π) | C. | ($\frac{3π}{2}$,$\frac{4035π}{2}$) | D. | (π,2017π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
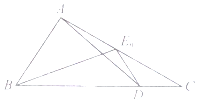 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BC}=3\overrightarrow{DC}$,${E_n}(n∈{N^*})$为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)•\overrightarrow{{E_n}D}$,其中实数列{an}中,an>0,a1=1,则a5=( )
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BC}=3\overrightarrow{DC}$,${E_n}(n∈{N^*})$为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)•\overrightarrow{{E_n}D}$,其中实数列{an}中,an>0,a1=1,则a5=( )| A. | 46 | B. | 30 | C. | 242 | D. | 161 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com