
| A. | 3 | B. | 5 | C. | $\frac{8\sqrt{14}}{7}$ | D. | 3$\sqrt{5}$ |
分析 类比点P(x0,y0)到直线Ax+By+C=0的距离d=$\frac{|A{x}_{0}+B{y}_{0}+C|}{\sqrt{{A}^{2}+{B}^{2}}}$,可知在空间中,d=$\frac{|2+8+3+3|}{\sqrt{1+4+9}}$=$\frac{8\sqrt{14}}{7}$.
解答 解:类比点P(x0,y0)到直线Ax+By+C=0的距离d=$\frac{|A{x}_{0}+B{y}_{0}+C|}{\sqrt{{A}^{2}+{B}^{2}}}$,
可知在空间中,
点(2,4,1)到平面x+2y+3z+3=0的距离d=$\frac{|2+8+3+3|}{\sqrt{1+4+9}}$=$\frac{8\sqrt{14}}{7}$.
故选C.
点评 类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $2\sqrt{2}-\sqrt{3}$ | C. | $\sqrt{2}-1$ | D. | $2-\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
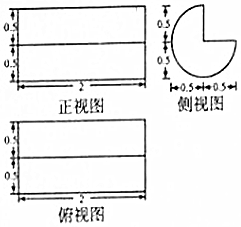 某同学在运动场所发现一实心椅子,其三视图如图所示(俯视图是圆的一部分及该圆的两条互相垂直的半径,有关尺寸如图,单位:m),经了解,建造该类椅子的平均成本为240元/m3,那么该椅子的建造成本约为(π≈3.14)( )
某同学在运动场所发现一实心椅子,其三视图如图所示(俯视图是圆的一部分及该圆的两条互相垂直的半径,有关尺寸如图,单位:m),经了解,建造该类椅子的平均成本为240元/m3,那么该椅子的建造成本约为(π≈3.14)( )| A. | 94.20元 | B. | 240.00元 | C. | 282.60元 | D. | 376.80元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $-\frac{π}{6}$ | D. | $-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com