
分析 (1)当a=1时,求导数,求出切线的斜率,即可求函数y=$\frac{g(x)}{f(x)}$在点(1,0)处的切线方程;
(2)设函数G(x)=a(x2-x)-lnx,且G(1)=0,分类讨论,即可,求实数a的取值范围.
解答 解:(1)当a=1时,函数y=$\frac{g(x)}{f(x)}$=$\frac{lnx}{x}$,
∴y′=$\frac{1-lnx}{{x}^{2}}$,
∴x=1时,y′=1,
∴函数y=$\frac{g(x)}{f(x)}$在点(1,0)处的切线方程为y=x-1;
(2)设函数G(x)=a(x2-x)-lnx,且G(1)=0.
G′(x)=$\frac{2a{x}^{2}-ax-1}{x}$
①当a≤0时,有G(2)=2a-ln2<0,不成立,
②当a<0时,(i)a≥1时,G′(x)=$\frac{2a{x}^{2}-ax-1}{x}$,当x≥1时,G′(x)≥0
所以G(x)在(0,+∞)上是单调增函数,所以G(x)≥G(1)=0
(ii)0<a<1时,设h(x)=2ax2-ax-1,h(1)=a-1<0,
所以存在x0,使得x∈(1,0)时,h(x)<0,∴G′(x)<0,G(x)<G(1)=0不成立
综上所述a≥1.
点评 考查基本初等函数求导公式,商的导数的计算公式,考查导数的几何意义,以及函数单调性定义,构造函数的方法.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
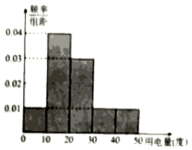 供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )
供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )| A. | 11月份人均用电量人数最多的一组有400人 | |
| B. | 11月份人均用电量不低于20度的有500人 | |
| C. | 11月份人均用电量为25度 | |
| D. | 在这1000位居民中任选1位协助收费,选到的居民用电量在30,40)一组的概率为$\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
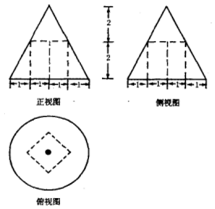
| A. | $\frac{10π}{3}-4$ | B. | $\frac{10π}{3}-8$ | C. | $\frac{16π}{3}-4$ | D. | $\frac{16π}{3}-8$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | $\frac{8\sqrt{14}}{7}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com