
���� ��1����˫����E�IJ����������˫����E����ͨ����Ϊ$\frac{{x}^{2}}{3}-{y}^{2}=1$���Ӷ����ֱ��l��ֱ������ϵ�еķ��̣��ɴ������l�ļ����귽�̣�
��2��������A��O��F��P�ĵ㹲Բ�ȼ���P�ǵ�A��O��Fȷ����Բ����ΪԲC��CΪԲ�ģ���ֱ��l�Ľ��㣨����ԭ��O�����߶�AFΪԲC��ֱ����A�ǹ�F��l��ֱ��ֱ����y��Ľ��㣬�Ӷ�C�İ뾶Ϊ2��Բ�ĵļ�����Ϊ��2��$\frac{��}{3}$�����ɴ��������P�ļ����꣮
��� �⣺��1����˫����E�IJ�������Ϊ$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{cos��}}\\{y=tan��}\end{array}\right.$����Ϊ��������
��$\frac{{x}^{2}}{3}=\frac{1}{co{s}^{2}��}$��${y}^{2}=ta{n}^{2}��=\frac{si{n}^{2}��}{co{s}^{2}��}$��
��$\frac{{x}^{2}}{3}-{y}^{2}$=$\frac{1}{co{s}^{2}��}-\frac{si{n}^{2}��}{co{s}^{2}��}$=1��
��˫����E����ͨ����Ϊ$\frac{{x}^{2}}{3}-{y}^{2}=1$��
��ֱ��l��ֱ������ϵ�еķ���Ϊy=$\frac{\sqrt{3}}{3}x$�����ԭ�㣬��б��Ϊ$\frac{��}{6}$��
��l�ļ����귽��Ϊ$��=\frac{��}{6}$��
��2��������A��O��F��P�ĵ㹲Բ�ȼ���P�ǵ�A��O��Fȷ����Բ����ΪԲC��CΪԲ�ģ���ֱ��l�Ľ��㣨����ԭ��O����
��AO��OF�����߶�AFΪԲC��ֱ����
�ɣ���֪��|OF|=2��
��A�ǹ�F��l��ֱ��ֱ����y��Ľ��㣬
���AFO=$\frac{��}{3}$��|AF|=4��
����ԲC�İ뾶Ϊ2��Բ�ĵļ�����Ϊ��2��$\frac{��}{3}$����
��ԲC�ļ����귽��Ϊ$��=4cos��\frac{��}{3}-�ȣ�$��
��ʱ����P�ļ�����Ϊ��4cos��$\frac{��}{3}-\frac{��}{6}$����$\frac{��}{6}$��������2$\sqrt{3}$��$\frac{��}{6}$����
���� ���⿼��ֱ�ߵļ����귽�̵��������ļ�����������е��⣬����ʱҪ�������⣬ע��������̡�ֱ�����귽�̡������귽�̻�����ʽ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
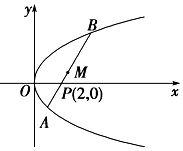 ��ͼ����ֱ֪��l����P��2��0����б��Ϊ$\frac{4}{3}$��ֱ��l��������y2=2x�ཻ��A��B���㣬���߶�AB���е�ΪM����
��ͼ����ֱ֪��l����P��2��0����б��Ϊ$\frac{4}{3}$��ֱ��l��������y2=2x�ཻ��A��B���㣬���߶�AB���е�ΪM�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | $\frac{1}{2}$ | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com