
分析 a1=1,an=Sn-1,(n≥2),可得a2=S1=a1=1,an+1=Sn,an+1-an=an,即an+1=2an.再利用等比数列的通项公式即可得出.
解答 解:∵a1=1,an=Sn-1,(n≥2),∴a2=S1=a1=1,an+1=Sn,an+1-an=an,即an+1=2an.
∴n≥2时,数列{an}是等比数列,首项为1,公比为2,∴${a}_{n}={2}^{n-2}$.
∴an=$\left\{\begin{array}{l}{1,n=1}\\{{2}^{n-2},n≥2}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{1,n=1}\\{{2}^{n-2},n≥2}\end{array}\right.$.
点评 本题考查了数列递推关系、等比数列的通项公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 减少7.84% | B. | 增加7.84% | C. | 减少9.5% | D. | 增加 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,$\frac{2}{x}$+lnx>0 | B. | ?x∈R,$\frac{2}{x}$+lnx≥0 | ||
| C. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0<0 | D. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
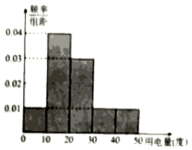 供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )
供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )| A. | 11月份人均用电量人数最多的一组有400人 | |
| B. | 11月份人均用电量不低于20度的有500人 | |
| C. | 11月份人均用电量为25度 | |
| D. | 在这1000位居民中任选1位协助收费,选到的居民用电量在30,40)一组的概率为$\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分条件 | B. | 必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
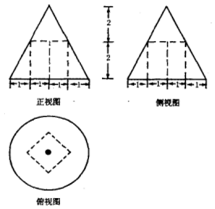
| A. | $\frac{10π}{3}-4$ | B. | $\frac{10π}{3}-8$ | C. | $\frac{16π}{3}-4$ | D. | $\frac{16π}{3}-8$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 600或900 | B. | 900或560 | C. | 900 | D. | 600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com