
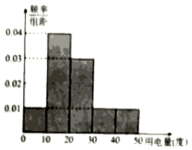
 ���粿�Ŷ�ij����1000λ����2016��11�·��˾��õ��������ͳ �ƺ��˾��õ�����Ϊ0��10����10��20����20��30����30��40����40��50]���飬�����õ����ҵ�Ƶ�ʷֲ�ֱ��ͼ��������˵��������ǣ�������
���粿�Ŷ�ij����1000λ����2016��11�·��˾��õ��������ͳ �ƺ��˾��õ�����Ϊ0��10����10��20����20��30����30��40����40��50]���飬�����õ����ҵ�Ƶ�ʷֲ�ֱ��ͼ��������˵��������ǣ�������| A�� | 11�·��˾��õ�����������һ����400�� | |
| B�� | 11�·��˾��õ���������20�ȵ���500�� | |
| C�� | 11�·��˾��õ���Ϊ25�� | |
| D�� | ����1000λ��������ѡ1λЭ���շѣ�ѡ���ľ����õ�����30��40��һ��ĸ���Ϊ$\frac{1}{10}$ |
���� ����Ƶ�ʷֲ�ֱ��ͼ�����11�·��˾��õ�����������һ�飬�ж�A��ȷ��
����11�·��˾��õ���������20�ȵ�Ƶ����Ƶ�����ж�B��ȷ��
����11�·��˾��õ�����ֵ���ж�C����
���������ѡ1λЭ���շѣ��õ�����[30��40��һ���Ƶ�ʣ��ж�D��ȷ��
��� �⣺����Ƶ�ʷֲ�ֱ��ͼ֪��
11�·��˾��õ�����������һ����[10��20������1000��0.04��10=400�ˣ�A��ȷ��
11�·��˾��õ���������20�ȵ�Ƶ���ǣ�0.03+0.01+0.01����10=0.5����1000��0.5=500�ˣ���B��ȷ��
11�·��˾��õ���Ϊ5��0.1+15��0.4+25��0.3+35��0.1+45��0.1=22����C����
����1000λ��������ѡ1λЭ���շѣ��õ�����[30��40��һ���Ƶ��Ϊ0.1��
��������ĸ���Ϊ$\frac{1}{10}$����D��ȷ��
��ѡ��C��
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ��Ӧ�����⣬�ǻ����⣮


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1��2��4} | B�� | {2��3��4} | C�� | {0��2��4} | D�� | {0��2��3��4} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
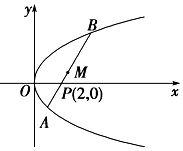 ��ͼ����ֱ֪��l����P��2��0����б��Ϊ$\frac{4}{3}$��ֱ��l��������y2=2x�ཻ��A��B���㣬���߶�AB���е�ΪM����
��ͼ����ֱ֪��l����P��2��0����б��Ϊ$\frac{4}{3}$��ֱ��l��������y2=2x�ཻ��A��B���㣬���߶�AB���е�ΪM�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -3 | C�� | ��3 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
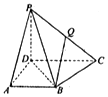 ������P-ABCD�У�PD��ƽ��ABCD������ABCD��ֱ�����Σ�AD��DC��AB��DC��DC=2AB����QΪ��PC��һ�㣬$\overrightarrow{PQ}$=��$\overrightarrow{PC}$
������P-ABCD�У�PD��ƽ��ABCD������ABCD��ֱ�����Σ�AD��DC��AB��DC��DC=2AB����QΪ��PC��һ�㣬$\overrightarrow{PQ}$=��$\overrightarrow{PC}$�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com