
分析 令y=ln(x+1)-ax-b-1,求出导数,分类讨论,进而得到b≥-lna+a-2,可得$\frac{b}{a}$≥1-$\frac{lna}{a}$-$\frac{2}{a}$,通过导数求出单调区间和极值、最值,进而得到$\frac{b}{a}$的最小值.
解答 解:令y=ln(x+1)-ax-b-1,则y′=$\frac{1}{x+1}$-a,
若a≤0,则y′>0恒成立,x>-1时函数递增,无最值.
若a>0,由y′=0得:x=$\frac{1-a}{a}$,
当-1<x<$\frac{1-a}{a}$时,y′>0,函数递增;
当x>$\frac{1-a}{a}$时,y′<0,函数递减.
则x=$\frac{1-a}{a}$处取得极大值,也为最大值-lna+a-b-2,
∴-lna+a-b-2≤0,
∴b≥-lna+a-2,
∴$\frac{b}{a}$≥1-$\frac{lna}{a}$-$\frac{2}{a}$,
令t=1-$\frac{lna}{a}$-$\frac{2}{a}$,
∴t′=$\frac{1+lna}{{a}^{2}}$,
∴(0,e-1)上,t′<0,(e-1,+∞)上,t′>0,
∴a=e-1,tmin=1-e.
∴$\frac{b}{a}$的最小值为1-e.
故答案为:1-e.
点评 本题考查不等式的恒成立问题注意转化为求函数的最值问题,运用导数判断单调性,求极值和最值是解题的关键,属于中档题


科目:高中数学 来源: 题型:选择题
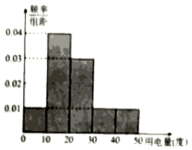 供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )
供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )| A. | 11月份人均用电量人数最多的一组有400人 | |
| B. | 11月份人均用电量不低于20度的有500人 | |
| C. | 11月份人均用电量为25度 | |
| D. | 在这1000位居民中任选1位协助收费,选到的居民用电量在30,40)一组的概率为$\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p>1 | B. | p≥1 | C. | p<1 | D. | p≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 600或900 | B. | 900或560 | C. | 900 | D. | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com