
分析 (1)求出函数的导数,利用导数为0,求解极值点,然后判断求解极值即可.
(2)利用导函数的符号,结合基本不等式或函数的导数求解函数的最值,推出结果即可.
解答 解:(1)∵f(x)=x2-(2-a)x-(2-a)lnx,x>0
∴$f'(x)=2x-(2-a)-\frac{2-a}{x}=\frac{{2{x^2}-(2-a)x-(2-a)}}{x}$,
因为a=1,令$f'(x)=\frac{{2{x^2}-x-1}}{x}$=0得x=1或x=$-\frac{1}{2}$(舍去)…(3分)
又因为,当0<x<1时,f'(x)<0;x>1时,f'(x)>0
所以x=1时,函数f(x)有极小值f(1)=0…(6分)
(2)若f'(x)>0,在x>0上恒成立,则2x2-(2-a)x-(2-a)>0恒成立,
∴$a>\frac{{-2{x^2}+2x+2}}{x+1}=6-2[{(x+1)+\frac{1}{x+1}}]$恒成立…(9分)
而当x>0时∵$[{(x+1)+\frac{1}{x+1}}]>2$.
检验知,a=2时也成立∴a≥2…(12分)
[或:令$g(x)=\frac{{-2{x^2}+2x+2}}{x+1}$,∴$g'(x)=\frac{-2x(x+2)}{{{{(x+1)}^2}}}$,∵x>0,∴g'(x)<0-----(9分)
所以,函数g(x)在定义域上为减函数
所以g(x)<g(0)=2
检验知,a=2时也成立∴a≥2…(12分).
点评 本题考查函数的导数的综合应用,函数的极值以及函数的单调性与函数的最值的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
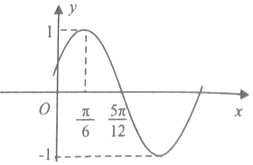 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
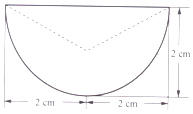 某零件的正视图与侧视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是底边上高为1cm的等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是( )
某零件的正视图与侧视图均是如图所示的图形(实线组成半径为2cm的半圆,虚线是底边上高为1cm的等腰三角形的两腰),俯视图是一个半径为2cm的圆(包括圆心),则该零件的体积是( )| A. | $\frac{4}{3}πc{m^3}$ | B. | $\frac{8}{3}πc{m^3}$ | C. | 4πcm3 | D. | $\frac{20}{3}πc{m^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com