
分析 (1)根据指数函数以及二次根式的性质求出a的范围即可;
(2)根据函数的值域的范围,得到关于a的方程,求出a的范围即可.
解答 解:(1)若f(x)的定义域为R,
由2x>0,则$\frac{a}{{2}^{x}}$>0,则a>0,
则f(x)=$\sqrt{{2}^{x}+\frac{a}{{2}^{x}}-2}$≥$\sqrt{2\sqrt{a}-2}$≥0,
解得:a≥1,
故a的范围是[1,+∞);
(2)若f(x)的值域为[0,+∞),
则f(x)=$\sqrt{{2}^{x}+\frac{a}{{2}^{x}}-2}$≥$\sqrt{2\sqrt{a}-2}$≥0,
由2$\sqrt{a}$-2=0,解得:a=1.
点评 本题考查了函数的定义域、值域问题,考查指数函数的性质以及基本不等式的性质,是一道中档题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | p>1 | B. | p≥1 | C. | p<1 | D. | p≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{5}{2},\frac{11}{3}}]$ | B. | $[{\frac{1}{2},\frac{3}{4}}]$ | C. | $({0,\frac{1}{2}}]$ | D. | $({0,\frac{11}{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | (-∞,0) | C. | (0,2) | D. | [2,+∞] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
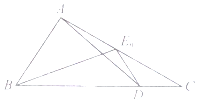 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BC}=3\overrightarrow{DC}$,${E_n}(n∈{N^*})$为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)•\overrightarrow{{E_n}D}$,其中实数列{an}中,an>0,a1=1,则a5=( )
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BC}=3\overrightarrow{DC}$,${E_n}(n∈{N^*})$为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)•\overrightarrow{{E_n}D}$,其中实数列{an}中,an>0,a1=1,则a5=( )| A. | 46 | B. | 30 | C. | 242 | D. | 161 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com