
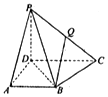
 在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是直角梯形,AD⊥DC,AB∥DC,DC=2AB,设Q为棱PC上一点,$\overrightarrow{PQ}$=λ$\overrightarrow{PC}$
在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是直角梯形,AD⊥DC,AB∥DC,DC=2AB,设Q为棱PC上一点,$\overrightarrow{PQ}$=λ$\overrightarrow{PC}$分析 (1)设PD的中点为F,连接qF,证明四边形FABq是平行四边形.利用直线与平面平行的判定定理证明Bq∥平面PAD.
(2)以D为原点,DA,DC,DP所在直线为x,y,z轴建立空间直角坐标系,求出相关点的坐标,平面PBD的法向量.平面QBD的法向量,通过二面角结合数量积求解λ即可.
解答 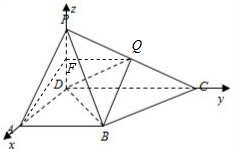 (1)证明:设PD的中点为F,连接F,
(1)证明:设PD的中点为F,连接F,
∵点Q,F分别是△PCD的中点,
∴QF∥CD,且QF=$\frac{1}{2}$CD,
∴QF∥AB,且QF=AB,
∴四边形FABQ是平行四边形.
∴BQ∥AF,又AF?平面PAD,BQ?平面PAD,
∴BQ∥平面PAD.
(2)解:以D为原点,DA,DC,DP所在直线为x,y,z轴建立空间直角坐标系,
则P(0,0,1),C(0,2,0),A(1,0,0),B(1,1,0).
令Q(x0,y0,z0),∵$\overrightarrow{PQ}$=λ$\overrightarrow{PC}$∴,Q(0,2λ,1-λ),
∵BC⊥平面PBD,
∴平面PBD的法向量为$\overrightarrow{BC}$=(-1,1,0).
设平面QBD的法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{x=-y}\\{z=\frac{2λ}{λ-1}y}\end{array}\right.$.令y=1,得$\overrightarrow{m}$=(-1,1,$\frac{2λ}{λ-1}$).
若二面角Q-BD-P为45°,
则$\frac{2}{\sqrt{2}•\sqrt{2+(\frac{2λ}{λ-1})^{2}}}$=$\frac{\sqrt{2}}{2}$,
解得λ=-1±$\sqrt{2}$,
∵Q在PC上,0<λ<1.∴$λ=\sqrt{2}-1$.
点评 本题考查直线与平面平行的判定定理的应用,二面角的平面角的求解与应用,考查空间想象能力以及计算能力.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,$\frac{2}{x}$+lnx>0 | B. | ?x∈R,$\frac{2}{x}$+lnx≥0 | ||
| C. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0<0 | D. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
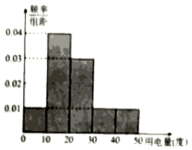 供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )
供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )| A. | 11月份人均用电量人数最多的一组有400人 | |
| B. | 11月份人均用电量不低于20度的有500人 | |
| C. | 11月份人均用电量为25度 | |
| D. | 在这1000位居民中任选1位协助收费,选到的居民用电量在30,40)一组的概率为$\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分条件 | B. | 必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
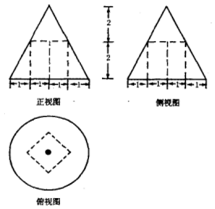
| A. | $\frac{10π}{3}-4$ | B. | $\frac{10π}{3}-8$ | C. | $\frac{16π}{3}-4$ | D. | $\frac{16π}{3}-8$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com