
分析 (1)f(x)=2即3x-$\frac{1}{{3}^{x}}$=2,先解3x,再解x值,注意3x>0;
(2)不等式3t•f(2t)+mf(t)≥0恒成立,通过整理变形转化为32t+1+m≥0恒成立,分离参数m后转化为求函数最值问题解决
解答 解:(1)f(x)=2即3x-$\frac{1}{{3}^{x}}$=2,得32x-2×3x-1=0,∴3x=1±$\sqrt{2}$,
又3x>0,∴3x=1+$\sqrt{2}$,
∴x=log3(1+$\sqrt{2}$).
(2)∵3t•f(2t)+mf(t)≥0,
∴3t(32t-3-2t)+m(3t-3-t)≥0,
∵t∈[1,2],
∴32t+1+m≥0恒成立,即m≥-(32t+1)恒成立,
问题等价于m大于等于-(32t+1)的最大值-10,
∴m≥-10,
因此m的取值范围为[-10,+∞).
点评 本题考查函数恒成立问题及指数方程的求解,考查学生的分析问题解决问题的能力,恒成立问题往往转化为求函数最值问题解决,或分离参数后再求函数最值.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-8] | B. | (-∞,-8]∪[0,+∞) | C. | (-∞,-4) | D. | [-8,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3)∪(2,+∞) | B. | (-∞,-3) | C. | (-3,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,4} | B. | {2,3,4} | C. | {0,2,4} | D. | {0,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
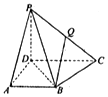 在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是直角梯形,AD⊥DC,AB∥DC,DC=2AB,设Q为棱PC上一点,$\overrightarrow{PQ}$=λ$\overrightarrow{PC}$
在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是直角梯形,AD⊥DC,AB∥DC,DC=2AB,设Q为棱PC上一点,$\overrightarrow{PQ}$=λ$\overrightarrow{PC}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com