练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．用0，1，2，3，4，5 组成没有重复的三位数，其中偶数共有（　　）
    A．24个B．30个C．52个D．60个

    分析 根据题意，按照个位数字的不同，分2种情况讨论：①、个位数字为0，在1、2、3、4、5 这5个数中任取2个，安排在十位、百位，由排列数公式可得其情况数目，②、个位数字为2或4，分析百位、十位数字的取法数目，由乘法原理可得此时的情况数目，进而由分类计数原理计算可得答案．

    解答 解：根据题意，要求组成三位偶数，其个位数字为0、2、4，则分2种情况讨论：
    ①、个位数字为0，在1、2、3、4、5 这5个数中任取2个，安排在十位、百位，有A52=20种情况，
    ②、个位数字为2或4，有2种情况，
    由于0不能在百位，百位数字在其余4个数字中任取1个，有4种情况，
    十位数字在剩下的4个数字中任取1个，有4种情况，
    则有2×4×4=32种情况，
    则有20+32=52种情况，即其中偶数有52个；
    故选：C．

    点评 本题考查排列、组合的应用，需要注意特殊数位上的数，比如，最高位不能是0，偶数的个位必须是，0、2、4这些数，再根据乘法原理解答即可

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    17．填空题：方程$\root{3}{x}|{sinπx}|=x-3\root{3}{x}$的解的个数为11个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=$\left\{\begin{array}{l}{{3}^{x}-\frac{1}{{3}^{x}}，x≥0}\\{0，x＜0}\end{array}\right.$
    （1）若f（x）=2，求x的值；
    （2）若3x•f（2t）+mf（t）≥0对于t∈[1，2]恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．张君四年前买了50000元的某种基金，收益情况是前两年每年递减20%，后两年每年递增20%，则现在的价值与原来价值比较，变化的情况是（　　）
    A．减少7.84%B．增加7.84%C．减少9.5%D．增加

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是（　　）
    A．若m⊥α，m∥n，n∥β，则 α⊥βB．若α∥β，m?α，n?β，则 m∥n
    C．若m⊥n，m?α，n?β，则α⊥βD．若α⊥β，m?α，n?β，则m⊥n

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知球O是的棱长为1的正方体ABCD-A1B1C1D1的内切球，则平面ACD1截球O的截面面积为（　　）
    A．πB．$\frac{π}{2}$C．$\frac{π}{3}$D．$\frac{π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．如图所示，程序框图输出的结果是（　　）
    A．55B．89C．144D．233

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．命题“?x0∈R，$\frac{2}{{x}_{0}}$+lnx0≤0”的否定是（　　）
    A．?x∈R，$\frac{2}{x}$+lnx＞0B．?x∈R，$\frac{2}{x}$+lnx≥0
    C．?x0∈R，$\frac{2}{{x}_{0}}$+lnx0＜0D．?x0∈R，$\frac{2}{{x}_{0}}$+lnx0＞0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知简单组合体的三视图如图所示，则此简单组合体的体积为（　　）
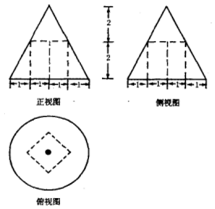
    A．$\frac{10π}{3}-4$B．$\frac{10π}{3}-8$C．$\frac{16π}{3}-4$D．$\frac{16π}{3}-8$

    查看答案和解析>>

    同步练习册答案