
| A. | (-∞,-8] | B. | (-∞,-8]∪[0,+∞) | C. | (-∞,-4) | D. | [-8,4) |
分析 方法一:令3x=t>0由条件可得a=$\frac{{t}^{2}+4t+4}{-t}$=-4-(t+$\frac{4}{t}$),利用基本不等式和不等式的性质求得实数a的取值范围,
方法二,由题意可得方程 t2+(4+a)•t+4=0 有正数解,根据判别式非负可得①式,再由两根之积等于4>0,可得 $\frac{4+a}{2}$>0,得到②式,由①和②求得实数a的取值范围.
解答 解:方法一:令3x=t>0,则关于x的方程9x+(4+a)•3x+4=0 即 t2+(4+a)t+4=0 有正实数解.
故 a=$\frac{{t}^{2}+4t+4}{-t}$=-4-(t+$\frac{4}{t}$),
由基本不等式可得 t+$\frac{4}{t}$≥4,当且仅当t=$\frac{4}{t}$时,等号成立,故-(t+$\frac{4}{t}$)≤-4,故-4-(t+$\frac{4}{t}$)≤-8,
即a≤-8,
方法二:△=(4+a)2-16≥0,∴a≤-8 或a≥0 ①.
再由两根之积等于4>0,可得 $\frac{4+a}{2}$>0,∴a<-4 ②.
结合①②可得 a≤-8
故选:A
点评 本题考查方程有解问题、基本不等式求最值问题,同时考查转化思想和换元法,属于中档题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
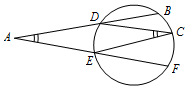 所谓弧的度数指的是弧所对的圆心角的度数,如图,$\widehat{BC}$,$\widehat{CF}$的度数分别为62°,68°,则∠BAF+∠DCE=65°.
所谓弧的度数指的是弧所对的圆心角的度数,如图,$\widehat{BC}$,$\widehat{CF}$的度数分别为62°,68°,则∠BAF+∠DCE=65°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | a>b>c | C. | c>a>b | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 月份 | 煤气使用量/m3 | 煤气费/元 |
| 7 | 4 | 4 |
| 8 | 25 | 14 |
| 9 | 35 | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 减少7.84% | B. | 增加7.84% | C. | 减少9.5% | D. | 增加 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,$\frac{2}{x}$+lnx>0 | B. | ?x∈R,$\frac{2}{x}$+lnx≥0 | ||
| C. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0<0 | D. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com