
| A. | 3 | B. | -3 | C. | ±3 | D. | -1 |
分析 根据题意,由向量$\overrightarrow{a}$的坐标,可得λ$\overrightarrow{a}$=(3λ,4λ),又由λ$\overrightarrow{a}$的坐标,可得μ=2λ,又由|λ$\overrightarrow{a}$|=5,结合向量模的公式,可得(3λ)2+(4λ)2=25,计算可得λ的值,进而可得μ的值,计算可得λ+μ的值,即可得答案.
解答 解:根据题意,向量$\overrightarrow{a}$=(3,4),则λ$\overrightarrow{a}$=(3λ,4λ),
又由λ$\overrightarrow{a}$=(3λ,2μ),则有4λ=2μ,即μ=2λ,
又由|λ$\overrightarrow{a}$|=5,则有(3λ)2+(4λ)2=25,
解可得λ=±1,
当λ=1时,μ=2λ=2,此时λ+μ=3,
当λ=-1时,μ=2λ=-2,此时λ+μ=-3,
即λ+μ=±3;
故选:C.
点评 本题考查向量的坐标运算,涉及向量的数乘运算,关键是求出λ、μ的关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
| 月份 | 煤气使用量/m3 | 煤气费/元 |
| 7 | 4 | 4 |
| 8 | 25 | 14 |
| 9 | 35 | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,$\frac{2}{x}$+lnx>0 | B. | ?x∈R,$\frac{2}{x}$+lnx≥0 | ||
| C. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0<0 | D. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
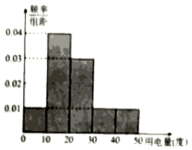 供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )
供电部门对某社区1000位居民2016年11月份人均用电情况进行统 计后,按人均用电量分为0,10),10,20),20,30),30,40),40,50]五组,整理得到如右的频率分布直方图,则下列说法错误的是( )| A. | 11月份人均用电量人数最多的一组有400人 | |
| B. | 11月份人均用电量不低于20度的有500人 | |
| C. | 11月份人均用电量为25度 | |
| D. | 在这1000位居民中任选1位协助收费,选到的居民用电量在30,40)一组的概率为$\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com