解:(1)由S
n=n
2+4n,
当n=1时,a
1=S
1=1
2+4=5;
当n≥2时,a
n=S
n-S
n-1=n
2+4n-(n-1)
2-4(n-1)=2n+3.
∴当n∈N
*时,a
n=2n+3. (3分)
又b
n+1=2b
n+1,b
1=1,即b
n+1+1=2(b
n+1),可得
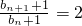
,
∴数列{b
n+1}是以2为首项,以2为公比的等比数列,
∴b
n+1=2×2
n-1=2
n,b
n=2
n-1. (6分)
(2)由(1)得c
n=
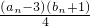
=n•2
n-1.
T
n=1×2
0+2×2+3×2
2+…+n•2
n-1,…①.
2T
n=1×2
1+2×2
2+3×2
3+…+n•2
n,…②.
由①-②得-T
n=1+2+2
2+2
3+2
4+…+2
n-1-n•2
n=

-n•2
n,
∴T
n=(n-1)•2
n+1. (12分)
分析:(1)由S
n=n
2+4n,求出a
1,当n≥2时,a
n=S
n-S
n-1,求出a
n.利用b
n+1=2b
n+1,b
1=1,判断数列{b
n+1}是以2为首项,以2为公比的等比数列,然后求解b
n.
(2)利用c
n=
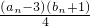
,求出c
n,利用错位相减法求出数列{c
n}的前n项和T
n.
点评:本题考查数列求和,数列的判定,递推关系式的应用,考查计算能力,转化思想.

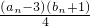 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.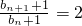 ,
,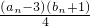 =n•2n-1.
=n•2n-1. -n•2n,
-n•2n,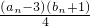 ,求出cn,利用错位相减法求出数列{cn}的前n项和Tn.
,求出cn,利用错位相减法求出数列{cn}的前n项和Tn.

 名校课堂系列答案
名校课堂系列答案