Question

【题目】如图，在五面体中，已知平面，，，，．

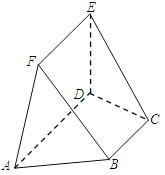
（1）求证：；

（2）求三棱锥的体积．

Answer 1

【答案】（1）详见解析，（2）

【解析】

试题分析：（1）证明线线平行，一般思路为利用线面平行的性质定理与判定定理进行转化. 因为，平面，平面，所以平面，又平面，平面平面，所以．（2）求三棱锥的体积，关键是找寻高.可由面面垂直性质定理探求，因为平面，所以有面平面，则作就可得平面.证明平面过程也可从线线垂直证线面垂直.确定是三棱锥的高之后，可利用三棱锥的体积公式.

试题解析：

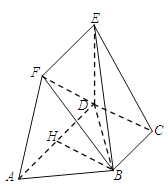
（1）因为，平面，平面，

所以平面， 3分

又平面，平面平面，

所以． 6分

（2）在平面内作于点，

因为平面，平面，所以，

又，平面，，

所以平面，

所以是三棱锥的高． 9分

在直角三角形中，，，所以，

因为平面，平面，所以，

又由（1）知，，且，所以，所以， 12分

所以三棱锥的体积． 14分