
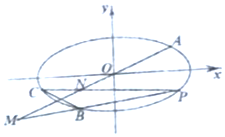
 如图,在平面直角坐标系xOy中,已知A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上不同的三点,$A(\sqrt{10},\frac{{\sqrt{10}}}{2})$,B(-2,-2),C在第三象限,线段BC的中点在直线OA上.
如图,在平面直角坐标系xOy中,已知A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上不同的三点,$A(\sqrt{10},\frac{{\sqrt{10}}}{2})$,B(-2,-2),C在第三象限,线段BC的中点在直线OA上.分析 (1)将A,B坐标代入椭圆方程,求出a,b,即可求椭圆的标准方程;
(2)设点C(m,n)(m<0,n<0),则BC中点为($\frac{m-2}{2}$,$\frac{n-2}{2}$),求得直线OA的方程,利用点C在椭圆上,即可求点C的坐标;
(3)求出M,N的纵坐标,利用点C在椭圆上,结合向量的数量积公式,即可求得结论.
解答 解:(1)由已知,将$A(\sqrt{10},\frac{{\sqrt{10}}}{2})$,B(-2,-2)代入椭圆方程:$\left\{\begin{array}{l}{\frac{10}{{a}^{2}}+\frac{\frac{10}{4}}{{b}^{2}}=1}\\{\frac{4}{{a}^{2}}+\frac{4}{{b}^{2}}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}^{2}=20}\\{{b}^{2}=5}\end{array}\right.$,
∴椭圆的标准方程为$\frac{{x}^{2}}{20}+\frac{{y}^{2}}{5}=1$; …(4分)
(2)解:设点C(m,n)(m<0,n<0),则BC中点为($\frac{m-2}{2}$,$\frac{n-2}{2}$).
由已知,求得直线OA的方程:x-2y=0,从而m=2n-2.①
又∵点C在椭圆上,
∴m2+4n2=20.②
由①②,解得:n=2(舍),n=-1,从而m=-4.
∴点C的坐标为(-4,-1).…(8分)
(3)证明:设P(x0,y0),M(2y1,y1),N(2y2,y2).
∵P,B,M三点共线,则$\frac{{y}_{1}+2}{2{y}_{1}+2}$=$\frac{{y}_{0}+2}{2{x}_{0}+2}$整理得y1=$\frac{2({x}_{0}-{y}_{0})}{2{y}_{0}+2-{x}_{0}}$.…(10分)
∵P,C,N三点共线,则$\frac{{y}_{2}+1}{2{y}_{2}+4}$=$\frac{{y}_{0}+1}{{x}_{0}+4}$,整理得y2=$\frac{{x}_{0}-4{y}_{0}}{2{y}_{0}-2-{x}_{0}}$.…(12分)
∵点C在椭圆上,
∴x02+4y02=20,x02=20-4y02,
从而y1y2=$\frac{2({x}_{0}^{2}+4{y}_{0}^{2}-5{x}_{0}{y}_{0})}{{x}_{0}^{2}+4{y}_{0}^{2}-4{x}_{0}{y}_{0}-4}$=$\frac{2(20-5{x}_{0}{y}_{0})}{16-4{x}_{0}{y}_{0}}$=2×$\frac{5}{4}$=$\frac{5}{2}$. …(14分)
∴$\overrightarrow{OM}$•$\overrightarrow{ON}$=5y1y2=$\frac{25}{2}$.
∴$\overrightarrow{OM}$•$\overrightarrow{ON}$为定值,定值为$\frac{25}{2}$. …(16分)
点评 本题考查椭圆的方程,考查向量的数量积公式,直线的斜率公式,考查学生分析解决问题的能力,属于中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lna>b-1 | B. | lna<b-1 | C. | lna=b-1 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{24}$ | C. | $\frac{π}{4}$ | D. | $\frac{7π}{24}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com