
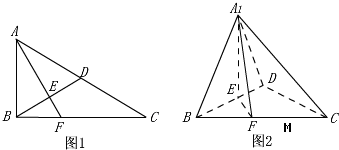
分析 (1)推导出A1E⊥BD,EF⊥BD,由此能证明BD⊥A1F.
(2)由DM∥EF,得DM∥平面A1EF,从而点M到平面A1EF的距离为DE,由此能求出结果.
解答 证明:(1)∵在Rt△ABC中,∠ABC=90°,D为AC中点,AE⊥BD于E(不同于D),
延长AE交BC于F,将△ABD沿BD折起,得到三棱锥A1-BCD,
∴A1E⊥BD,EF⊥BD,
∵A1E∩EF=E,∴BD⊥平面A1EF,
∵A1F?平面A1EF,
∴BD⊥A1F.
解:(2)∵D,M分别为AC,BD中点,
∴DM∥EF,
又EF?平面A1EF,DM?平面A1EF,
∴DM∥平面A1EF,
∴点M到平面A1EF的距离为DE,
∵图1中,AB=2,BC=2$\sqrt{3}$,∴AC=$\sqrt{4+12}$=4,
∴AB=AD=BD=2,∴DE=1,
∴点M到平面A1EF的距离为1.
点评 本题考查线线垂直的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y全不为0,则x2+y2≠0” | |
| B. | 若命题$p:?{x_0}∈R,{x_0}^2-{x_0}+1<0$,则?p:?x∉R,x2-x+1≥0 | |
| C. | 若命题“p或q”为真命题,则命题p和命题q均为真命题 | |
| D. | “x>3”是“x>2”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | [-1,0) | C. | (-1,+∞) | D. | {x|x≥-1,且x≠0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
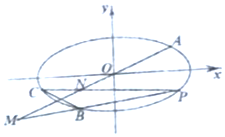 如图,在平面直角坐标系xOy中,已知A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上不同的三点,$A(\sqrt{10},\frac{{\sqrt{10}}}{2})$,B(-2,-2),C在第三象限,线段BC的中点在直线OA上.
如图,在平面直角坐标系xOy中,已知A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上不同的三点,$A(\sqrt{10},\frac{{\sqrt{10}}}{2})$,B(-2,-2),C在第三象限,线段BC的中点在直线OA上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com