考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:根据极值的定义,先对原函数求导数,然后令导函数等于0,求出方程的解,再根据极值的定义看在所求的点处能否取到极值,是极大值还是极小值.对于第二问,先对函数f(x)求导,然后求得f′(x)>0,和f′(x)<0的解,在这注意讨论a的取值.
解答:
解:(1)f(x)=
x3-x2-3x+3,所以f′(x)=x
2-2x-3.
∴解x
2-2x-3=0,得:x=-1或x=3,所以
x∈(-∞,-1)时,f′(x)>0;
x∈(-1,3)时,f′(x)<0;
x∈(3,+∞)时,f′(x)>0.
根据极值的定义知:x=-1时,f(x)取到极大值f(-1)=
;x=3时,f(x)取到极小值f(3)=-6.
(2)f′(x)=x
2-2x+a=(x-1)
2+a-1,∵a≤1,∴a-1≤0
∴若a-1=0,即a=1时f′(x)≥0,所以(-∞,+∞)是f(x)的单调增区间;
若a<1时,解(x-1)
2+a-1=0得:x=1±
,所以:
x∈(-∞,
1-)时,f′(x)>0,∴(-∞,
1-)是f(x)的单调增区间;
x∈(
1-,1+)时,f′(x)<0,∴[
1-,1+]是f(x)的单调减区间;
x∈(
1+,+∞)时,f′(x)>0,∴(
1+,+∞)是f(x)的单调增区间.
点评:考查极值的定义,只要理解极值的定义,第一问不难解出.第二问要注意一下讨论a的取值.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案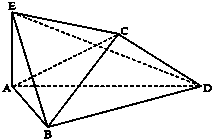 菱形ABCD边长为2,∠BAD=60°,将ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=
菱形ABCD边长为2,∠BAD=60°,将ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=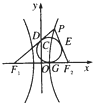 如图所示,已知P为双曲线
如图所示,已知P为双曲线