
【题目】已知函数![]() ,
,![]() .
.
(1)记![]() ,试判断
,试判断![]() 在区间
在区间![]() 内零点个数并说明理由;
内零点个数并说明理由;
(2)记(1)中的![]() 在
在![]() 内的零点为
内的零点为![]() ,
, ,若
,若![]() 在
在![]() 有两个不等实根
有两个不等实根![]()
![]() ,判断
,判断![]() 与
与![]() 的大小,并给出对应的证明.
的大小,并给出对应的证明.
【答案】(1)一个零点,理由见解析;(2)![]() ,证明见解析
,证明见解析
【解析】
(1)利用导数得到![]() 在区间
在区间![]() 上是增函数,
上是增函数,![]() ,
,![]() ,并且
,并且![]() 在
在![]() 上连续的,由零点定理即得解;(2)先求出当
上连续的,由零点定理即得解;(2)先求出当![]() 时,
时,![]() 是单调递增函数;当
是单调递增函数;当![]() 时,
时,![]() 是单调递减函数,转化成证明
是单调递减函数,转化成证明![]() ,即转化成证明
,即转化成证明![]() .
.
(1)由题意:![]() ,
,
那么![]() ,定义域为
,定义域为![]() ,
,![]() ,
,
由题设![]() ,故
,故![]() ,即
,即![]() 在区间
在区间![]() 上是增函数.
上是增函数.
那么![]() ,
,![]() ,并且
,并且![]() 在
在![]() 上连续的,
上连续的,
故根据零点存在定理,有![]() 在区间
在区间![]() 有且仅有唯一实根,即一个零点.
有且仅有唯一实根,即一个零点.
(2) ,
,
当![]() 时,
时,![]() 恒大于
恒大于![]() ,
,
所以当![]() 时,
时,![]() 是单调递增函数;
是单调递增函数;
当![]() 时,
时,![]() 恒小于
恒小于![]() ,
,![]() 是单调递减函数.
是单调递减函数.![]() 在
在![]() 有两个不等实根
有两个不等实根![]() ,
,
则![]() ,
,![]() ,显然:当
,显然:当![]() 时,
时,![]() .
.
要证明![]() ,即可证明
,即可证明![]() ,
,
而![]() 在
在![]() 时是单调递减函数.故证
时是单调递减函数.故证![]() .
.
又由![]() ,即可证:
,即可证:![]() .即
.即![]() ,(构造思想),
,(构造思想),
即![]() ,
,
令![]() ,由(1)可知:
,由(1)可知:![]() ,
,
那么:![]() ,
,
记![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;故
;故![]() ;
;
而![]() ;故
;故![]() ,而
,而![]() ,从而有:
,从而有:![]() ;
;
因此:![]() ,即
,即![]() 单增,从而
单增,从而![]() 时,
时,![]() ,
,
即![]() 成立.故得:
成立.故得:![]() .
.


科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则1<t<4且t≠![]() ;
;
②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;
④若C表示椭圆,且长轴在x轴上,则1<t<![]() .
.
其中正确的命题是________(把所有正确命题的序号都填在横线上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() ,
,![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)说明![]() 是哪一种曲线,并将
是哪一种曲线,并将![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)若直线![]() 的方程为
的方程为![]() ,设
,设![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() :
:![]() (
(![]() 为参数),
为参数),![]() 与
与![]() 相切于点
相切于点![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程及点
的极坐标方程及点![]() 的极坐标;
的极坐标;
(2)已知直线![]() :
:![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
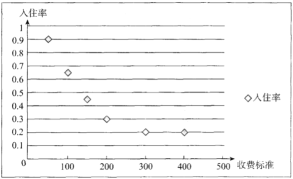
【题目】近年来,随着互联网技术的快速发展,共享经济覆盖的范围迅速扩张,继共享单车、共享汽车之后,共享房屋以“民宿”、“农家乐”等形式开始在很多平台上线.某创业者计划在某景区附近租赁一套农房发展成特色“农家乐”,为了确定未来发展方向,此创业者对该景区附近六家“农家乐”跟踪调查了![]() 天.得到的统计数据如下表,
天.得到的统计数据如下表,![]() 为收费标准(单位:元/日),
为收费标准(单位:元/日),![]() 为入住天数(单位:),以频率作为各自的“入住率”,收费标准
为入住天数(单位:),以频率作为各自的“入住率”,收费标准![]() 与“入住率”
与“入住率”![]() 的散点图如图
的散点图如图
x | 50 | 100 | 150 | 200 | 300 | 400 |
t | 90 | 65 | 45 | 30 | 20 | 20 |
(1)若从以上六家“农家乐”中随机抽取两家深入调查,记![]() 为“入住率”超过
为“入住率”超过![]() 的农家乐的个数,求
的农家乐的个数,求![]() 的概率分布列;
的概率分布列;
(2)令![]() ,由散点图判断
,由散点图判断![]() 与
与![]() 哪个更合适于此模型(给出判断即可,不必说明理由)?并根据你的判断结果求回归方程.(
哪个更合适于此模型(给出判断即可,不必说明理由)?并根据你的判断结果求回归方程.(![]() 结果保留一位小数)
结果保留一位小数)
(3)若一年按![]() 天计算,试估计收费标准为多少时,年销售额
天计算,试估计收费标准为多少时,年销售额![]()
![]() 入住率
入住率![]() 收费标准
收费标准![]() )
)
参考数据: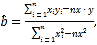
![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)某县一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨、硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨、硝酸盐15吨.先库存磷酸盐10吨、硝酸盐66吨,在此基础上生产这两种混合肥料.若生产1车皮甲种肥料产生的利润为10000元;生产1车皮乙种肥料产生的利润为5000元.那么分别生产甲、乙两种肥料各多少车皮能产生最大的利润?
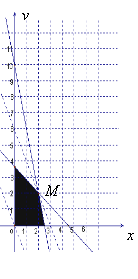
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第16届亚运会在中国广州进行,为了搞好接待工作,组委会招幕了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有![]() 人和
人和![]() 人喜爱运动,其余人不喜爱运动.
人喜爱运动,其余人不喜爱运动.
(1)根据以上数据完成以下![]() 列联表:
列联表:
喜爱运动 | 不喜爱运动 | 总计 | |
男 |
|
| |
女 |
|
| |
总计 |
|
(2)根据列联表的独立性检验,能否在犯错误的概率不超过![]() 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?
附:
|
|
|
|
|
|
|
|
|
|
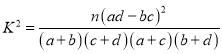 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com