
若函数 ,则对于不同的实数a,函数
,则对于不同的实数a,函数 的单调区间个数不可能是( )
的单调区间个数不可能是( )
| A.1个 | B.2个 | C.3个 | D.5个 |
B
解析试题分析:最高次项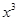 递增,无论a如何取值,当x---> +∞时,f(x)递增;
递增,无论a如何取值,当x---> +∞时,f(x)递增;
当x从左边-∞开始(当然没有开始)时, f(x)递增。
由于曲线是连续的,所以,(1)若中间连续递增,(a=0时)单调区间个数为1;
(2) 若中间只有一段递减,即增,减,增单调区间个数为3;
(3)若中间有2段递减,即增,减,增,减,增单调区间个数为5;
总之单调区间个数不可能为2。
另,无论x取何值,a取何值,原函数被分成三部分讨论(-∞,-1),[-1,1],(1,+∞).当a=0时,是一个单调区间,a不等于零时,三次函数,则不可能有两个单调区间 ,故选B 。
考点:函数的图象,应用导数研究函数的单调性。
点评:中档题,作为选择题,在解答过程中,可借助于就的函数的单调性,做出定性分析,简化解答过程。本题为选择题,不必“小题大作”。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com