
(本题满分50分)已知无穷数列![]() 满足
满足![]() ,
,![]() ,
, ![]() .
.
1)对于怎样的实数![]() 与
与![]() ,总存在正整数
,总存在正整数![]() ,使当
,使当![]() 时
时![]() 恒为常数?
恒为常数?
解析:1)我们有
![]() ,
,![]() (2.1)
(2.1)
所以,如果对某个正整数![]() ,有
,有![]() ,则必有
,则必有 ![]() , 且
, 且 ![]() .
.
如果该![]() ,我们得
,我们得
![]() 且
且 ![]() . ………………(10分) (2.2)
. ………………(10分) (2.2)
如果该![]() ,我们有
,我们有
![]() ,
, ![]() (2.3)
(2.3)
和
![]() ,
, ![]() (2.4)
(2.4)
将式(2.3)和(2.4)两端相乘,得
![]() ,
, ![]() (2.5)
(2.5)
由(2.5)递推,必有(2.2)或
![]() 且
且 ![]() . (2.6)
. (2.6)
反之,如果条件(2.2)或(2.6)满足,则当n≥2时,必有an=常数,且常数是1或-1.
2)由(2.3)和(2.4),我们得到
![]() ,
, ![]() (2.7)
(2.7)
记![]() , 则当
, 则当![]() 时,
时,
![]()
由此递推,我们得到
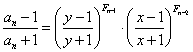 ,
, ![]() (2.8)
(2.8)
这里
![]() ,
,![]() ,
, ![]() . (2.9)
. (2.9)
由(2.9)解得
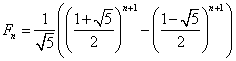 . (2.10)
. (2.10)
上式中的n还可以向负向延伸,例如
![]() .
.
这样一来,式(2.8)对所有的![]() 都成立.由(2.8)解得
都成立.由(2.8)解得
![]() ,
, ![]() . (2.11)
. (2.11)


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
(本题满分12分)
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中,![]() 还喜欢打羽毛球,
还喜欢打羽毛球,![]() 还喜欢打乒乓球,
还喜欢打乒乓球,![]() 还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分l4分)如图,一个小球从M处投入,通过管道自上而下落A或B或C。已知小球从每个叉口落入左右两个 管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到A,B,C,则分别设为l,2,3等奖.
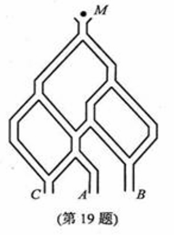 (I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量
(I)已知获得l,2,3等奖的折扣率分别为50%,70%,90%.记随变量![]() 为获得k(k=1,2,3)等奖的折扣率,求随机变量
为获得k(k=1,2,3)等奖的折扣率,求随机变量![]() 的分布列及期望
的分布列及期望![]() ;
;
(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量![]() 为获得1等奖或2等奖的人次,求
为获得1等奖或2等奖的人次,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com