
【题目】已知![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】从某大学中随机选取7名女大学生,其身高x(单位:cm)和体重y(单位:kg)数据如下表:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
身高x | 163 | 164 | 165 | 166 | 167 | 168 | 169 |
体重y | 52 | 52 | 53 | 55 | 54 | 56 | 56 |
(1)求y关于x的回归方程;
(2)利用(1)中的回归方程,分析这7名女大学生的身高和体重的变化,并预报一名身高为172cm的女大学生的体重.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司年会举行抽奖活动,每位员工均有一次抽奖机会.活动规则如下:一只盒子里装有大小相同的6个小球,其中3个白球,2个红球,1个黑球,抽奖时从中一次摸出3个小球,若所得的小球同色,则获得一等奖,奖金为300元;若所得的小球颜色互不相同,则获得二等奖,奖金为200元;若所得的小球恰有2个同色,则获得三等奖,奖金为100元.
(1)求小张在这次活动中获得的奖金数![]() 的概率分布及数学期望;
的概率分布及数学期望;
(2)若每个人获奖与否互不影响,求该公司某部门3个人中至少有2个人获二等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从4名男同学中选出2人,6名女同学中选出3人,并将选出的5人排成一排.
(1)共有多少种不同的排法?
(2)若选出的2名男同学不相邻,共有多少种不同的排法?(用数字表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为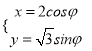 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求经过椭圆![]() 右焦点
右焦点![]() 且与直线
且与直线![]() 垂直的直线的极坐标方程;
垂直的直线的极坐标方程;
(2)若![]() 为椭圆
为椭圆![]() 上任意-点,当点
上任意-点,当点![]() 到直线
到直线![]() 距离最小时,求点
距离最小时,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com