
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,求证:
,求证:![]() ;
;
(Ⅲ)若![]() 对于
对于![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(Ⅱ)证明见解析;(Ⅲ)
;(Ⅱ)证明见解析;(Ⅲ)![]() .
.
【解析】
(Ⅰ)利用二次求导可得![]() ,所以
,所以![]() 在
在![]() 上为增函数,进而可得函数
上为增函数,进而可得函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(Ⅱ)利用导数可得
;(Ⅱ)利用导数可得![]() 在区间
在区间![]() 上存在唯一零点,所以函数
上存在唯一零点,所以函数![]() 在
在![]() 递减,在
递减,在![]() ,
,![]() 递增,则
递增,则![]() ,进而可证;(Ⅲ)条件等价于
,进而可证;(Ⅲ)条件等价于![]() 对于
对于![]() 恒成立,构造函数
恒成立,构造函数![]() ,利用导数可得
,利用导数可得![]() 的单调性,即可得到
的单调性,即可得到![]() 的最小值为
的最小值为![]() ,再次构造函数
,再次构造函数![]() (a)
(a)![]() ,
,![]() ,利用导数得其单调区间,进而求得最大值.
,利用导数得其单调区间,进而求得最大值.
(Ⅰ)当![]() 时,
时,![]() ,
,
则![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 在
在![]() 上为增函数,
上为增函数,
因为![]() ,所以当
,所以当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
即函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;
;
(Ⅱ)![]() ,
,
则令![]() ,则
,则![]() (1)
(1)![]() ,
,![]() ,
,
所以![]() 在区间
在区间![]() 上存在唯一零点,
上存在唯一零点,
设零点为![]() ,则
,则![]() ,且
,且![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() ,
,![]() ,
,![]() ,
,
所以函数![]() 在
在![]() 递减,在
递减,在![]() ,
,![]() 递增,
递增,
![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() ,
,
由于![]() ,
,![]() ,从而
,从而![]() ;
;
(Ⅲ)因为![]() 对于
对于![]() 恒成立,即
恒成立,即![]() 对于
对于![]() 恒成立,
恒成立,
不妨令![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() 的解为
的解为![]() ,
,
则当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
所以![]() 的最小值为
的最小值为![]() ,
,
则![]() ,
,
不妨令![]() (a)
(a)![]() ,
,![]() ,
,
则![]() (a)
(a)![]() ,解得
,解得![]() ,
,
所以当![]() 时,
时,![]() (a)
(a)![]() ,
,![]() (a)为增函数,
(a)为增函数,
当![]() 时,
时,![]() (a)
(a)![]() ,
,![]() (a)为减函数,
(a)为减函数,
所以![]() (a)的最大值为
(a)的最大值为![]() ,
,
则![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PC⊥平面ABCD,点M为PB中点,底面ABCD为梯形,AB∥CD,AD⊥CD,AD=CD=PC=![]() AB.
AB.
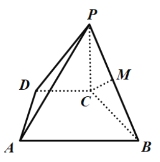
(1)证明:CM∥平面PAD;
(2)若四棱锥P-ABCD的体积为4,求点M到平面PAD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校设计了一个实验考察方案:考生从6道备选题中随机抽取3道题,按照题目要求独立完成全部实验操作,规定:至少正确完成其中的2道题便可通过.已知6道备选题中考生甲有4道能正确完成,2道题不能完成;考生乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(Ⅰ)求甲考生通过的概率
(Ⅱ)求甲乙两考生正确完成题数的概率分布列和数学期望;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年![]() 市加大雾霾治理的投入,空气质量与前几年相比有了很大改善,并于
市加大雾霾治理的投入,空气质量与前几年相比有了很大改善,并于![]() 年
年![]() 市入选中国空气优良城市
市入选中国空气优良城市![]() .已知该市设有
.已知该市设有![]() 个监测站用于监测空气质量指数(
个监测站用于监测空气质量指数(![]() ),其中在轻度污染区、中度污染区、重度污染区分别设有
),其中在轻度污染区、中度污染区、重度污染区分别设有![]() 、
、![]() 、
、![]() 个监测站,并以
个监测站,并以![]() 个监测站测得的
个监测站测得的![]() 的平均值为依据播报该市的空气质量.
的平均值为依据播报该市的空气质量.
(1)若某日播报的![]() 为
为![]() ,已知轻度污染区
,已知轻度污染区![]() 平均值为
平均值为![]() ,中度污染区
,中度污染区![]() 平均值为
平均值为![]() ,求重度污染区
,求重度污染区![]() 平均值;
平均值;
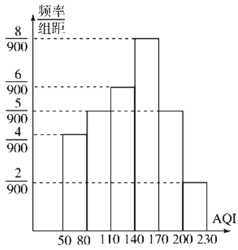
(2)如图是![]() 年
年![]() 月份
月份![]() 天的
天的![]() 的频率分布直方图,
的频率分布直方图,![]() 月份仅有
月份仅有![]() 天
天![]() 在
在![]() 内.
内.
①某校参照官方公布的![]() ,如果周日
,如果周日![]() 小于
小于![]() 就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
②环卫部门从![]() 月份
月份![]() 不小于
不小于![]() 的数据中抽取两天的数据进行研究,求抽取的这两天中
的数据中抽取两天的数据进行研究,求抽取的这两天中![]() 值在
值在![]() 的天数的概率.
的天数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面坐标系中![]() 中,已知直线l的参考方程为
中,已知直线l的参考方程为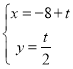 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为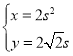 (s为参数).设P为曲线C上的动点,
(s为参数).设P为曲线C上的动点,
(Ⅰ)求直线l和曲线C的直角坐标方程;
(Ⅱ)求点P到直线l的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com