
【题目】近几年![]() 市加大雾霾治理的投入,空气质量与前几年相比有了很大改善,并于
市加大雾霾治理的投入,空气质量与前几年相比有了很大改善,并于![]() 年
年![]() 市入选中国空气优良城市
市入选中国空气优良城市![]() .已知该市设有
.已知该市设有![]() 个监测站用于监测空气质量指数(
个监测站用于监测空气质量指数(![]() ),其中在轻度污染区、中度污染区、重度污染区分别设有
),其中在轻度污染区、中度污染区、重度污染区分别设有![]() 、
、![]() 、
、![]() 个监测站,并以
个监测站,并以![]() 个监测站测得的
个监测站测得的![]() 的平均值为依据播报该市的空气质量.
的平均值为依据播报该市的空气质量.
(1)若某日播报的![]() 为
为![]() ,已知轻度污染区
,已知轻度污染区![]() 平均值为
平均值为![]() ,中度污染区
,中度污染区![]() 平均值为
平均值为![]() ,求重度污染区
,求重度污染区![]() 平均值;
平均值;
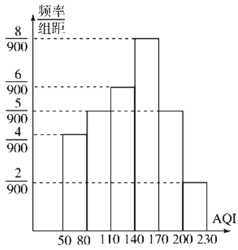
(2)如图是![]() 年
年![]() 月份
月份![]() 天的
天的![]() 的频率分布直方图,
的频率分布直方图,![]() 月份仅有
月份仅有![]() 天
天![]() 在
在![]() 内.
内.
①某校参照官方公布的![]() ,如果周日
,如果周日![]() 小于
小于![]() 就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
②环卫部门从![]() 月份
月份![]() 不小于
不小于![]() 的数据中抽取两天的数据进行研究,求抽取的这两天中
的数据中抽取两天的数据进行研究,求抽取的这两天中![]() 值在
值在![]() 的天数的概率.
的天数的概率.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)设重度污染区![]() 平均值为
平均值为![]() ,根据题意得出关于
,根据题意得出关于![]() 的等式,即可求得
的等式,即可求得![]() 的值;
的值;
(2)①根据频率分布直方图计算出![]() 不小于
不小于![]() 的天数,进而利用古典概型的概率公式和对立事件的概率公式可求得所求事件的概率;
的天数,进而利用古典概型的概率公式和对立事件的概率公式可求得所求事件的概率;
②记![]() 在
在![]() 上的
上的![]() 天的编号为
天的编号为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 在
在![]() 上的
上的![]() 天的编号为
天的编号为![]() 、
、![]() ,列举出所有的基本事件,利用古典概型的概率公式可求得所求事件的概率.
,列举出所有的基本事件,利用古典概型的概率公式可求得所求事件的概率.
(1)设重度污染区![]() 平均值为
平均值为![]() ,
,![]() ,
,![]() ;
;
(2)①![]() 在
在![]() 上的有
上的有![]() 天,
天,
![]() 在
在![]() 上的有
上的有![]() 天,
天,
![]() 在
在![]() 上的有
上的有![]() 天,
天,
所以![]() 月份
月份![]() 不小于
不小于![]() 的共
的共![]() 天.
天.
即能参加户外活动的概率为![]() ;
;
②由①![]() 在
在![]() 上的
上的![]() 天的编号为
天的编号为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 在
在![]() 上的
上的![]() 天的编号为
天的编号为![]() 、
、![]() ,
,
从![]() 天中抽取两天的基本事件有:
天中抽取两天的基本事件有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 种情况.
种情况.
满足条件的基本事件有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 种,
种,
所以,抽取的这两天中![]() 值在
值在![]() 的天数的概率为
的天数的概率为![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】某快递公司有两种发放薪水的方案:
方案一:底薪1800元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为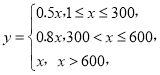
方案二:底薪2000元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为![]()
以下该公司某职工小甲在2019年9月份(30天)送快递的数据,
日送快递单数 | 11 | 13 | 14 | 15 | 16 | 18 |
天数 | 4 | 5 | 12 | 3 | 5 | 1 |
(1)从小甲日送快递单数大于15的六天中抽取两天,求这两天他送的快递单数恰好都为16单的概率.
(2)请你利用所学的统计学知识为小甲9月份选择合适的发放薪水的方案,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为纪念“五四运动”100周年,某校团委举办了中国共产主义青年团知识宣讲活动活动结束后,校团委对甲、乙两组各10名团员进行志愿服务次数调查,次数统计结果用茎叶图记录如下,乙组记录中有一个数据模糊,无法确认,在图中以![]() 表示.
表示.
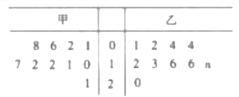
(1)若甲组服务次数的平均值不小于乙组服务次数的平均值,求图中![]() 所有可能的取值;
所有可能的取值;
(2)团委决定对甲、乙两组中服务次数超过15次的团员授予“优秀志愿者”称号设![]() ,现从所有“优秀志愿者”里任取3人,求其中乙组的人数
,现从所有“优秀志愿者”里任取3人,求其中乙组的人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市垃圾处理厂的垃圾年处理量(单位:千万吨)与资金投入量x(单位:千万元)有如下统计数据:
2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
资金投入量x(千万元) | 1.5 | 1.4 | 1.9 | 1.6 | 2.1 |
垃圾处理量y(千万吨) | 7.4 | 7.0 | 9.2 | 7.9 | 10.0 |
(1)若从统计的5年中任取2年,求这2年的垃圾处理量至少有一年不低于8.0(千万吨)的概率;
(2)由表中数据求得线性回归方程为![]() ,该垃圾处理厂计划2017年的垃圾处理量不低于9.0千万吨,现由垃圾处理厂决策部门获悉2017年的资金投入量约为1.8千万元,请你预测2017年能否完成垃圾处理任务,若不能,缺口约为多少千万吨?
,该垃圾处理厂计划2017年的垃圾处理量不低于9.0千万吨,现由垃圾处理厂决策部门获悉2017年的资金投入量约为1.8千万元,请你预测2017年能否完成垃圾处理任务,若不能,缺口约为多少千万吨?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月,北京世界园艺博览会开幕,为了保障园艺博览会安全顺利地进行,某部门将5个安保小组全部安排到指定的三个不同区域内值勤,则每个区域至少有一个安保小组的排法有( )
A.150种B.240种C.300种D.360种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车站每天上午发出两班客车,每班客车发车时刻和发车概率如下:第一班车:在8:00,8:20,8:40发车的概率分别为![]() ,
,![]() ,
,![]() ;第二班车:在9:00,9:20,9:40发车的概率分别为
;第二班车:在9:00,9:20,9:40发车的概率分别为![]() ,
,![]() ,
,![]() .两班车发车时刻是相互独立的,一位旅客8:10到达车站乘车.求:
.两班车发车时刻是相互独立的,一位旅客8:10到达车站乘车.求:
(1)该旅客乘第一班车的概率;
(2)该旅客候车时间(单位:分钟)的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com