
【题目】如图,在四棱锥P-ABCD中,PC⊥平面ABCD,点M为PB中点,底面ABCD为梯形,AB∥CD,AD⊥CD,AD=CD=PC=![]() AB.
AB.
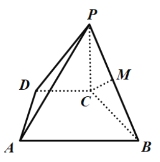
(1)证明:CM∥平面PAD;
(2)若四棱锥P-ABCD的体积为4,求点M到平面PAD的距离.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为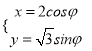 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求经过椭圆![]() 右焦点
右焦点![]() 且与直线
且与直线![]() 垂直的直线的极坐标方程;
垂直的直线的极坐标方程;
(2)若![]() 为椭圆
为椭圆![]() 上任意-点,当点
上任意-点,当点![]() 到直线
到直线![]() 距离最小时,求点
距离最小时,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD中,PC⊥底面ABCD,PC=CD=2,E为AB的中点,底面四边形ABCD满足∠ADC=∠DCB=90°,AD=1,BC=3.
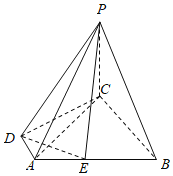
(Ⅰ)求证:平面PDE⊥平面PAC;
(Ⅱ)求直线PC与平面PDE所成角的正弦值;
(Ⅲ)求二面角D﹣PE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点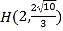 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的方程;
(Ⅱ)点![]() 在圆
在圆![]() 上,且
上,且![]() 在第一象限,过
在第一象限,过![]() 作
作![]() 的切线交椭圆于
的切线交椭圆于![]() 两点,问:
两点,问: ![]() 的周长是否为定值?若是,求出定值;若不是,说明理由.
的周长是否为定值?若是,求出定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司有两种发放薪水的方案:
方案一:底薪1800元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为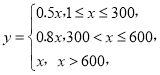
方案二:底薪2000元,设每月送快递![]() 单,提成(单位:元)为
单,提成(单位:元)为![]()
以下该公司某职工小甲在2019年9月份(30天)送快递的数据,
日送快递单数 | 11 | 13 | 14 | 15 | 16 | 18 |
天数 | 4 | 5 | 12 | 3 | 5 | 1 |
(1)从小甲日送快递单数大于15的六天中抽取两天,求这两天他送的快递单数恰好都为16单的概率.
(2)请你利用所学的统计学知识为小甲9月份选择合适的发放薪水的方案,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车站每天上午发出两班客车,每班客车发车时刻和发车概率如下:第一班车:在8:00,8:20,8:40发车的概率分别为![]() ,
,![]() ,
,![]() ;第二班车:在9:00,9:20,9:40发车的概率分别为
;第二班车:在9:00,9:20,9:40发车的概率分别为![]() ,
,![]() ,
,![]() .两班车发车时刻是相互独立的,一位旅客8:10到达车站乘车.求:
.两班车发车时刻是相互独立的,一位旅客8:10到达车站乘车.求:
(1)该旅客乘第一班车的概率;
(2)该旅客候车时间(单位:分钟)的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com