练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

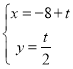    【题目】在平面坐标系中中，已知直线l的参考方程为（t为参数），曲线C的参数方程为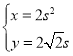（s为参数）.设P为曲线C上的动点，

    （Ⅰ）求直线l和曲线C的直角坐标方程；

    （Ⅱ）求点P到直线l的距离的最小值.

    【答案】（Ⅰ），（Ⅱ）

    【解析】

    （Ⅰ）由直线的参数方程为为参数），消去参数，可得普通方程．由曲线的参数方程为为参数）．消去参数，可得曲线直角坐标方程．（Ⅱ）设点，则为参数）．利用点到直线的距离公式可得：，利用二次函数的单调性即可得出最小值．

    （Ⅰ）由直线的参数方程为为参数），消去参数，可得：．

    所以直线直角坐标方程为．

    由曲线的参数方程为为参数）．消去参数，可得：．

    所以曲线直角坐标方程为．

    （Ⅱ）设点，则为参数）．

    则．

    当时取等号，此时，，

    所以点到直线的距离的最小值为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中．

    （Ⅰ）当时，求函数的单调区间；

    （Ⅱ）设，求证：；

    （Ⅲ）若对于恒成立，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某车站每天上午发出两班客车，每班客车发车时刻和发车概率如下：第一班车：在8:00，8:20，8:40发车的概率分别为，，；第二班车：在9:00，9:20，9:40发车的概率分别为，，．两班车发车时刻是相互独立的，一位旅客8:10到达车站乘车．求：

    （1）该旅客乘第一班车的概率；

    （2）该旅客候车时间（单位：分钟）的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和为，且满足，，设，则以下四个命题：（1）是等差数列；（2）中最大项是；（3）通项公式是；（4）.其中真命题的序号是______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某综艺节目为比较甲、乙两名选手的各项能力(指标值满分为5分，分值高者为优)，绘制了如图所示的六维能力雷达图，图中点A表示甲的创造力指标值为4，点B表示乙的空间能力指标值为3，则下面叙述正确的是

    A. 乙的记忆能力优于甲的记忆能力

    B. 乙的创造力优于观察能力

    C. 甲的六大能力整体水平优于乙

    D. 甲的六大能力中记忆能力最差

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）当时，求函数的单调区间；

    （2）若不等式对任意的正实数都成立，求实数的最大整数值.

    （3）当时，若存在实数且，使得，求证.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）当时，求曲线在点处的切线方程；

    （Ⅱ）求函数的单调区间；

    （Ⅲ）若对任意的，都有成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，底面是边长为2的菱形，是的中点．

    （1）证明：平面；

    （2）设是线段上的动点，当点到平面距离最大时，求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】抛物线C的顶点在坐标原点，对称轴为x轴，抛物线C过点A（4，4），过抛物线C的焦点F作倾斜角等于45°的直线l，直线l交抛物线C于M、N两点．

    （1）求抛物线C的方程；

    （2）求线段MN的长．

    查看答案和解析>>

    同步练习册答案