Question

【题目】已知椭圆C： 的右顶点A（2，0），且过点
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点B（1，0）且斜率为k1（k1≠0）的直线l于椭圆C相交于E，F两点，直线AE，AF分别交直线x=3于M，N两点，线段MN的中点为P，记直线PB的斜率为k2 ， 求证：k1k2为定值．

Answer 1

【答案】解：（Ⅰ）由题意可得a=2， + =1，
a2﹣b2=c2 ，
解得b=1，
即有椭圆方程为 +y2=1；
（Ⅱ）证明：设过点B（1，0）的直线l方程为：y=k1（x﹣1），
由 ，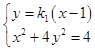
可得：（4k12+1）x2﹣8k12x+4k12﹣4=0，
因为点B（1，0）在椭圆内，所以直线l和椭圆都相交，
即△＞0恒成立．
设点E（x1 ， y1），F（x2 ， y2），
则x1+x2= ，x1x2= ．
因为直线AE的方程为：y= （x﹣2），
直线AF的方程为：y= （x﹣2），
令x=3，得M（3， ），N（3， ），
所以点P的坐标（3， （ + ））．
直线PB的斜率为k2= = （ + ）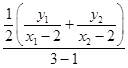
= =
= =﹣ ．
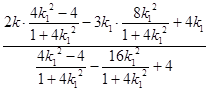所以k1k2为定值﹣ ．
【解析】（Ⅰ）由题意可得a=2，代入点 ，解方程可得椭圆方程；（Ⅱ）设过点B（1，0）的直线l方程为：y=k（x﹣1），由 ，可得（4k12+1）x2﹣8k12x+4k12﹣4=0，由已知条件利用韦达定理推导出直线PB的斜率k2=﹣ ，由此能证明kk′为定值﹣ ．