有两个投资项目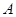
、
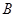，根据市场调查与预测，A项目的利润与投资成正比，其关系如图甲，B项目的利润与投资的算术平方根成正比，其关系如图乙.（注：利润与投资单位：万元）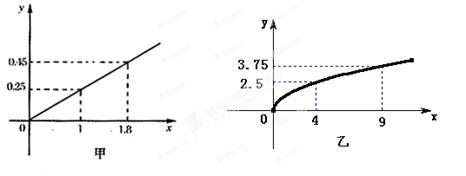
（1）分别将A、B两个投资项目的利润表示为投资x（万元）的函数关系式；
（2）现将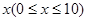
万元投资A项目, 10-x万元投资B项目.h(x)表示投资A项目所得利润与投资B项目所得利润之和.求h(x)的最大值,并指出x为何值时,h(x)取得最大值.
阅读快车系列答案科目：高中数学 来源： 题型：解答题
已知函数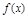
＝x2－4x＋a＋3，g(x)＝mx＋5－2m．
(Ⅰ)若方程f(x)=0在[－1，1]上有实数根，求实数a的取值范围；
(Ⅱ)当a＝0时，若对任意的x1∈[1，4]，总存在x2∈[1，4]，使f(x1)＝g(x2)成立，求实数m的取值范围；
(Ⅲ)若函数y＝f(x)（x∈[t，4]）的值域为区间D，是否存在常数t，使区间D的长度为7－2t？若存在，求出t的值；若不存在，请说明理由（注：区间[p，q]的长度为q－p）．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数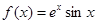
.
（Ⅰ）求函数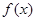
的单调区间；
（Ⅱ）如果对于任意的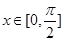
，
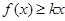总成立，求实数
的取值范围；
（Ⅲ）是否存在正实数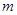
，使得：当
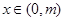时，不等式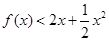
恒成立？请给出结论并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
若f(x)的定义域为[a,b]，值域为[a,b]（a<b），则称函数f(x)是[a,b]上的“四维光军”函数.
①设g(x)＝
x2－x+
是[1，b]上的“四维光军”函数，求常数b的值;
②问是否存在常数a，b（a>－2），使函数h(x)=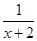
是区间[a,b]上的“四维光军”函数？若存在，求出a,b的值，否则，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车流速度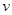
（单位：千米/小时）是车流密度
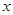（单位：辆/千米）的函数．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0千米/小时；当车流密度不超过20辆/千米时，车流速度为60千米/小时．研究表明：当
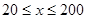时，车流速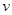度是车流密度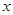的一次函数．
（Ⅰ）当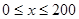
时，求函数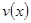
的表达式；
（Ⅱ）当车流密度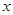为多大时，车流量（单位时间内通过桥上某观测点的车辆数，单位：辆/小时）
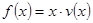可以达到最大，并求出最大值.（精确到1辆/小时）
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某企业有两个生产车间，分别位于边长是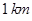
的等边三角形
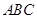的顶点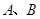
处（如图），现要在边
上的
点建一仓库，某工人每天用叉车将生产原料从仓库运往车间，同时将成品运回仓库．已知叉车每天要往返
车间5次，往返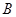
车间20次，设叉车每天往返的总路程为
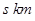.（注：往返一次即先从仓库到车间再由车间返回仓库）
(Ⅰ）按下列要求确定函数关系式：
①设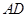
长为
，将
表示成的函数关系式；
②设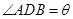
，将表示成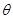
的函数关系式.
(Ⅱ）请你选用(Ⅰ）中一个合适的函数关系式，求总路程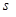 
的最小值，并指出点的位置．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某商场在店庆一周年开展“购物折上折活动”：商场内所有商品按标价的八折出售，折后价格每满500元再减100元．如某商品标价为1500元，则购买该商品的实际付款额为1500×0.8-200=1000（元）．设购买某商品得到的实际折扣率
．设某商品标价为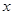
元，购买该商品得到的实际折扣率为
．
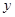（Ⅰ）写出当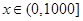
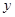时，关于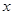的函数解析式，并求出购买标价为1000元商品得到的实际折扣率；
（Ⅱ）对于标价在［2500,3500］的商品，顾客购买标价为多少元的商品，可得到的实际折扣率低于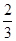
？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
;（Ⅱ）当A项目投入3.75万元，B项目投入6.25万元时，最大利润为
万元.
万元，A项目的利润为
万元，B项目的利润为
万元。
，由图知
故
2分
所以
4分
6分
，则
10分
时，
此时
11分
，其中常数a > 0．
上是减函数；
，
，求
的范围； （2）不等式
对任意
恒成立，求实数
的取值范围。