
已知函数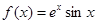 .
.
(Ⅰ)求函数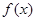 的单调区间;
的单调区间;
(Ⅱ)如果对于任意的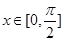 ,
,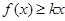 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;
(Ⅲ)是否存在正实数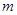 ,使得:当
,使得:当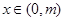 时,不等式
时,不等式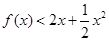 恒成立?请给出结论并说明理由.
恒成立?请给出结论并说明理由.
(Ⅰ)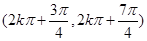 ;(Ⅱ)
;(Ⅱ)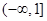 ;(Ⅲ)存在,
;(Ⅲ)存在,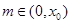 .
.
解析试题分析:(Ⅰ)先求 ,利用辅助角公式,函数
,利用辅助角公式,函数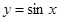 的性质求得;(Ⅱ)构造新函数,用导数法求解,需要对
的性质求得;(Ⅱ)构造新函数,用导数法求解,需要对 进行分类讨论;(Ⅲ)探索性问题,构造新函数
进行分类讨论;(Ⅲ)探索性问题,构造新函数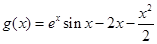 ,用导数法解题.
,用导数法解题.
试题解析:(Ⅰ)由于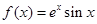 ,
,
所以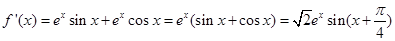 . (2分)
. (2分)
当 ,即
,即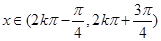 时,
时,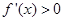 ;
;
当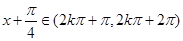 ,即
,即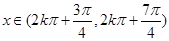 时,
时,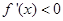 .
.
所以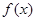 的单调递增区间为
的单调递增区间为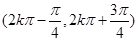
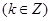 ,
,
单调递减区间为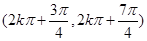
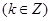 . (4分)
. (4分)
(Ⅱ)令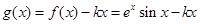 ,要使
,要使 总成立,只需
总成立,只需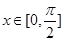 时
时 .
.
对 求导得
求导得 ,
,
令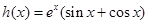 ,则
,则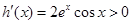 ,(
,(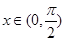 )
)
所以 在
在 上为增函数,所以
上为增函数,所以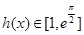 . (6分)
. (6分)
对 分类讨论:
分类讨论:
① 当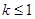 时,
时,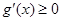 恒成立,所以
恒成立,所以 在
在 上为增函数,
上为增函数,
所以 ,即
,即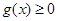 恒成立;
恒成立;
② 当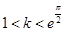 时,
时,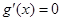 在上有实根
在上有实根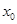 ,因为
,因为 在
在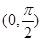 上为增函数,
上为增函数,
所以当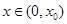 时,
时,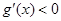 ,所以
,所以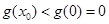 ,不符合题意;
,不符合题意;
③ 当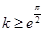 时,
时,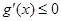 恒成立,所以
恒成立,所以 在
在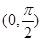 上为减函数,则
上为减函数,则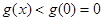 ,不符合题意.
,不符合题意.
综合①②③可得,所求的实数 的取值范围是
的取值范围是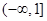 . (9分)
. (9分)
(Ⅲ)存在正实数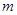 使得当
使得当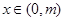 时,不等式
时,不等式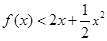 恒成立.
恒成立.
理由如下:令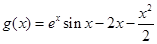 ,要使
,要使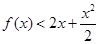 在
在 上恒成立,只需
上恒成立,只需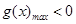 . (10分)
. (10分)
因为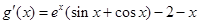 ,且
,且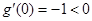 ,
,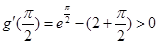 ,
,
所以存在正实数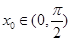 ,使得
,使得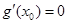 ,
,


科目:高中数学 来源: 题型:解答题
某社区有甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.
(1)设在甲家租一张球台开展活动 小时的收费为
小时的收费为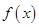 元
元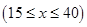 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动 小时的收费为
小时的收费为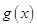 元
元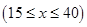 .试求
.试求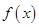 和
和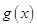 .
.
(2)问:小张选择哪家比较合算?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有两个投资项目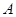 、
、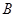 ,根据市场调查与预测,A项目的利润与投资成正比,其关系如图甲,B项目的利润与投资的算术平方根成正比,其关系如图乙.(注:利润与投资单位:万元)
,根据市场调查与预测,A项目的利润与投资成正比,其关系如图甲,B项目的利润与投资的算术平方根成正比,其关系如图乙.(注:利润与投资单位:万元)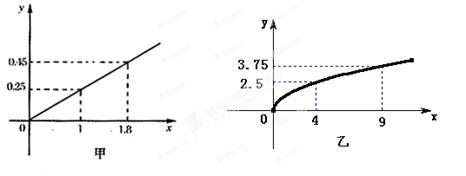
(1)分别将A、B两个投资项目的利润表示为投资x(万元)的函数关系式;
(2)现将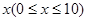 万元投资A项目, 10-x万元投资B项目.h(x)表示投资A项目所得利润与投资B项目所得利润之和.求h(x)的最大值,并指出x为何值时,h(x)取得最大值.
万元投资A项目, 10-x万元投资B项目.h(x)表示投资A项目所得利润与投资B项目所得利润之和.求h(x)的最大值,并指出x为何值时,h(x)取得最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com