
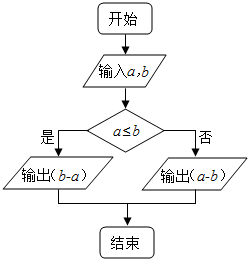
 对任意的非零实数a,b,若a?b的运算原理如图所示,且min{a,b,c}表示a,b,c中的最小值,则2?min{1,log0.30.1,30.1}的值为( )
对任意的非零实数a,b,若a?b的运算原理如图所示,且min{a,b,c}表示a,b,c中的最小值,则2?min{1,log0.30.1,30.1}的值为( )| A. | 0 | B. | 1 | C. | $2-log_{0.3}^{0.1}$ | D. | 2-30.1 |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算分段函数y=$\left\{\begin{array}{l}{b-a}&{a≤b}\\{a-b}&{a>b}\end{array}\right.$函数值,并输出,比较1,log0.30.1,30.1的大小,即可得解.
解答 解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:
该程序的作用是计算分段函数y=$\left\{\begin{array}{l}{b-a}&{a≤b}\\{a-b}&{a>b}\end{array}\right.$函数值,
∵30.1>1,log0.30.1>1,可得:min{1,log0.30.1,30.1}=1,
∵2>1,
∴y=2-1=1.
故选:B.
点评 本题考查程序框图的应用和数值的大小比较,一般情况下,含有指数与对数比较大小时,借助中间值“0”“1”比较,属于基础题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,5] | B. | (-∞,2]∪[5,+∞) | C. | (-∞,3]∪[5,+∞) | D. | [3,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
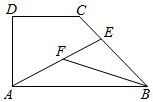 如图,在直角梯形ABCD中,AB=2AD=2DC=2,E为BC边上一点,$\overrightarrow{BC}$=3$\overrightarrow{EC}$,F为线段AE的中点,则$\overrightarrow{AE}$•$\overrightarrow{BF}$=$-\frac{14}{9}$.
如图,在直角梯形ABCD中,AB=2AD=2DC=2,E为BC边上一点,$\overrightarrow{BC}$=3$\overrightarrow{EC}$,F为线段AE的中点,则$\overrightarrow{AE}$•$\overrightarrow{BF}$=$-\frac{14}{9}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com