
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)求出函数的导数,问题转化为ex≥a恒成立,从而求出a的范围即可;
(3)求出f(x)的最小值,问题转化为只需证明gmax(a)≤2,根据函数的单调性证明即可.
解答 解:(1)函数的定义域:R …(1分)
当a=e时,f'(x)=ex-e…(2分)
令f'(x)=0解得x=1,
令f′(x)>0,解得:x>1,令f′(x)<0,解得:x<1,
所以f(x)的单调递减区间是(-∞,1),递增区间是(1,+∞)…(5分)
(2)因为f(x)在定义域内单调递增,
则f'(x)=ex-a≥0在R上恒成立…(6分),
即ex≥a恒成立,ex>0…(7分)所以a≤0.…(8分)
(3)证明:f'(x)=ex-a
当a>0时令f'(x)=0,解得x=lna,
令f′(x)>0,解得:x>lna,令f′(x)<0,解得:x<lna,
∴f(x)在(-∞,lna)递减,在(lna,+∞)递增,
所以g(a)=fmin(x)=f(lna)=a-alna+1…(9分)
要证明g(a)≤2,则只需证明gmax(a)≤2…(10分)
而g'(a)=-lna令g'(a)=0,解得a=1,…(11分)
令g′(a)>0,解得:a<1,令g′(a)<0,解得:a>1,
所以gmax(a)=g(1)=2≤2成立.
∴g(a)≤2…(12分).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道中档题.


科目:高中数学 来源: 题型:填空题
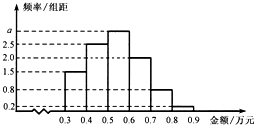 某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.直方图中的a=3.
某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.直方图中的a=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{sin0.5}$ | B. | sin0.5 | C. | 2sin1 | D. | $\frac{1}{cos0.5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足$\overrightarrow{OP}$=m$\overrightarrow{OA}$+$\overrightarrow{OB}$(m为常数).
已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足$\overrightarrow{OP}$=m$\overrightarrow{OA}$+$\overrightarrow{OB}$(m为常数).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有且只有一个平面β,使得m⊥β,且n?β | |
| B. | 有无数个平面β,使得m⊥β,且n?β | |
| C. | 不存在平面β,使得m⊥β,且n?β | |
| D. | 至多有一个平面β,使得m⊥β,且n?β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com