
【题目】在平面直角坐标系xOy中,已知过点![]() 的圆
的圆![]() 和直线
和直线![]() 相切,且圆心在直线
相切,且圆心在直线![]() 上.
上.
(1)求圆![]() 的标准方程;
的标准方程;
(2)点![]() ,圆
,圆![]() 上是否存在点
上是否存在点![]() ,使
,使![]()
![]() 若存在,求出点
若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴右侧的图象,如图所示.
轴右侧的图象,如图所示.
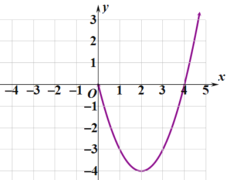
(1)画出函数![]() 在
在![]() 轴左侧的图象,根据图象写出函数
轴左侧的图象,根据图象写出函数![]() 在
在![]() 上的单调区间;
上的单调区间;
(2)求函数![]() 在
在![]() 上的解析式;
上的解析式;
(3)解不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值与最小值.
的最大值与最小值.
(2)是否存在过点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,使得
,使得![]() ?若存在,求直线
?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知对任意平面向量![]() ,把
,把![]() 绕其起点沿逆时针方向旋转
绕其起点沿逆时针方向旋转![]() 角得到向量
角得到向量![]() ,叫做把点
,叫做把点![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() 角得到点
角得到点![]() .
.
(1)已知平面内点![]() ,点
,点![]() .把点
.把点![]() 绕点
绕点![]() 沿顺时针方向旋转
沿顺时针方向旋转![]() 后得到点
后得到点![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设平面内曲线![]() 上的每一点绕坐标原点沿逆时针方向旋转
上的每一点绕坐标原点沿逆时针方向旋转![]() 后得到的点的轨迹是曲线
后得到的点的轨迹是曲线![]() ,求原来曲线
,求原来曲线![]() 的方程,并求曲线
的方程,并求曲线![]() 上的点到原点距离的最小值.
上的点到原点距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机作为客户端越来越为人们所青睐,通过手机实现衣食住行消费已经成为一种主要的消费方式.在某市,随机调查了200名顾客购物时使用手机支付的情况,得到如下的2×2列联表,已知从使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
(I)根据已知条件完成2×2列联表,并根据此资料判断是否有99.5%的把握认为“市场购物用手机支付与年龄有关”?
2×2列联表:
青年 | 中老年 | 合计 | |
使用手机支付 | 120 | ||
不使用手机支付 | 48 | ||
合计 | 200 |
(Ⅱ)现采用分层抽样的方法从这200名顾客中按照“使用手机支付”和“不使用手机支付”抽取一个容量为10的样本,再从中随机抽取3人,求这三人中“使用手机支付”的人数的分布列及期望.
附:![]()
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上的三点,
上的三点,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,当
,当![]() 的中点恰为点
的中点恰为点![]() 时,判断
时,判断![]() 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com