
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 过点
过点![]() 且倾斜角为
且倾斜角为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,若曲线
轴正半轴为极轴建立极坐标系,若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)若![]() ,求直线
,求直线![]() 的直角坐标方程.
的直角坐标方程.
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A的值;
(2)若![]() ,
, ![]() ,求△ABC的面积S.
,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且![]() ,
, ![]() .
.

求证:(1)直线DE![]() 平面A1C1F;
平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 为抛物线
为抛物线![]() 上不同的两点,且
上不同的两点,且![]() ,点
,点![]()
![]() 且
且![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)过![]() 轴上一点
轴上一点 ![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 在
在![]() 的准线上的射影分别为
的准线上的射影分别为![]() ,
,![]() 为
为![]() 的焦点,若
的焦点,若![]() ,求
,求![]() 中点
中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,是一个半圆柱与多面体![]() 构成的几何体,平面
构成的几何体,平面![]() 与半圆柱的下底面共面,且
与半圆柱的下底面共面,且![]() ,
, ![]() 为弧
为弧![]() 上(不与
上(不与![]() 重合)的动点.
重合)的动点.
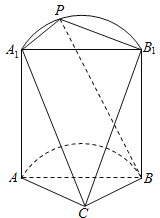
(1)证明: ![]() 平面
平面![]() ;
;
(2)若四边形![]() 为正方形,且
为正方形,且![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设min{m,n}表示m,n二者中较小的一个,已知函数f(x)=x2+8x+14,g(x)=![]() (x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
(x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
A.-4B.-3C.-2D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请120名同学每人随机写下一个x,y都小于1的正实数对
的值:先请120名同学每人随机写下一个x,y都小于1的正实数对![]() ,再统计其中x,y能与1构成钝角三角形三边的数对
,再统计其中x,y能与1构成钝角三角形三边的数对![]() 的个数m,最后根据统计个数m估计
的个数m,最后根据统计个数m估计![]() 的值.如果统计结果是
的值.如果统计结果是![]() ,那么可以估计
,那么可以估计![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com