
【题目】某产品自生产并投入市场以来,生产企业为确保产品质量,决定邀请第三方检测机构对产品进行质量检测,并依据质量指标![]() 来衡量产品的质量.当
来衡量产品的质量.当![]() 时,产品为优等品;当
时,产品为优等品;当![]() 时,产品为一等品;当
时,产品为一等品;当![]() 时,产品为二等品.第三方检测机构在该产品中随机抽取500件,绘制了这500件产品的质量指标
时,产品为二等品.第三方检测机构在该产品中随机抽取500件,绘制了这500件产品的质量指标![]() 的条形图.用随机抽取的500件产品作为样本,估计该企业生产该产品的质量情况,并用频率估计概率.
的条形图.用随机抽取的500件产品作为样本,估计该企业生产该产品的质量情况,并用频率估计概率.
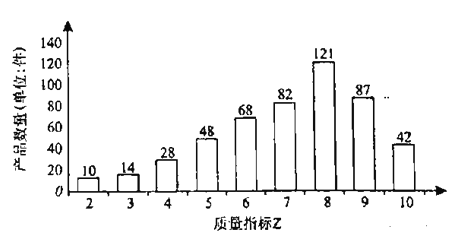
(1)从该企业生产的所有产品中随机抽取1件,求该产品为优等品的概率;
(2)现某人决定购买80件该产品.已知每件成本1000元,购买前,邀请第三方检测机构对要购买的80件产品进行抽样检测.买家、企业及第三方检测机构就检测方案达成以下协议:从80件产品中随机抽出4件产品进行检测,若检测出3件或4件为优等品,则按每件1600元购买,否则按每件1500元购买,每件产品的检测费用250元由企业承担.记企业的收益为![]() 元,求
元,求![]() 的分布列与数学期望;
的分布列与数学期望;
(3)商场为推广此款产品,现面向意向客户推出“玩游戏,送大奖”活动.客户可根据抛硬币的结果,操控机器人在方格上行进,已知硬币出现正、反面的概率都是![]() ,方格图上标有第0格、第1格、第2格、……、第50格.机器人开始在第0格,客户每掷一次硬币,机器人向前移动一次,若掷出正面,机器人向前移动一格(从
,方格图上标有第0格、第1格、第2格、……、第50格.机器人开始在第0格,客户每掷一次硬币,机器人向前移动一次,若掷出正面,机器人向前移动一格(从![]() 到
到![]() ),若掷出反面,机器人向前移动两格(从
),若掷出反面,机器人向前移动两格(从![]() 到
到![]() ),直到机器人移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束,若机器人停在“胜利大本营”,则可获得优惠券.设机器人移到第
),直到机器人移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束,若机器人停在“胜利大本营”,则可获得优惠券.设机器人移到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并解释此方案能否吸引顾客购买该款产品.
是等比数列,并解释此方案能否吸引顾客购买该款产品.
【答案】(1)![]() (2)分布见解析,数学期望为41500;(3)证明见解析,此方案能吸引顾客购买该款产品.
(2)分布见解析,数学期望为41500;(3)证明见解析,此方案能吸引顾客购买该款产品.
【解析】
(1)根据条形图,可得优等品的频率为![]() ,进而可得其概率;(2)计算出
,进而可得其概率;(2)计算出![]() 的值可以为47000,39000,计算出其分别对应的概率,得到分布列,进而可得期望;(3)首先易得
的值可以为47000,39000,计算出其分别对应的概率,得到分布列,进而可得期望;(3)首先易得![]() ,
,![]() ,根据题意可得
,根据题意可得![]() ,化简即可得
,化简即可得![]() ,即
,即![]() 为等比数列,利用累加法可得
为等比数列,利用累加法可得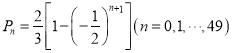 ,再分别计算出获胜和失败的概率,比较大小即可得结果.
,再分别计算出获胜和失败的概率,比较大小即可得结果.
(1)根据条形图可知,优等品的频率为![]() ,用频率估计概率,则任取一件产品为优等品的概率为
,用频率估计概率,则任取一件产品为优等品的概率为![]() .
.
(2)由(1)任取一件产品为优等品的概率为![]() ,
,
由题意![]() ,或
,或
![]()
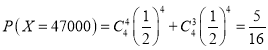 ;
;
 .
.
故![]() 的分布列为:
的分布列为:
| 47000 | 39000 |
|
|
|
所以数学期望![]() .
.
(3)机器人在第0格为必然事件,![]() ,第一次掷硬币出现正面,机器人移到第1格,其概率
,第一次掷硬币出现正面,机器人移到第1格,其概率![]() .机器人移到第
.机器人移到第![]() 格的情况只有两种:
格的情况只有两种:
①先到第![]() 格,又出现反面,其概率
格,又出现反面,其概率![]() ,
,
②先到第![]() 格,又出现正面,其概率
格,又出现正面,其概率![]() .
.
所以![]() ,故
,故![]()
所以![]() 时,数列
时,数列![]() 为首项
为首项![]() ,
,
公比为![]() 的等比数列.
的等比数列.
所以![]() ,
,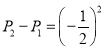 ,
, ,
,![]() ,
, ,
,
以上各式累加,得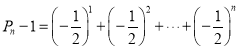 ,
,
所以
所以获胜概率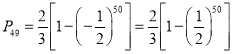 ,
,
失败概率
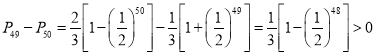 ,所以获胜概率更大,
,所以获胜概率更大,
故此方案能吸引顾客购买该款产品.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】在股票市场上,投资者常根据股价![]() 每股的价格
每股的价格![]() 走势图来操作,股民老张在研究某只股票时,发现其在平面直角坐标系内的走势图有如下特点:每日股价
走势图来操作,股民老张在研究某只股票时,发现其在平面直角坐标系内的走势图有如下特点:每日股价![]() 元
元![]() 与时间
与时间![]() 天
天![]() 的关系在ABC段可近似地用函数
的关系在ABC段可近似地用函数![]() 的图象从最高点A到最低点C的一段来描述
的图象从最高点A到最低点C的一段来描述![]() 如图
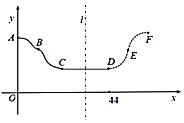
如图![]() ,并且从C点到今天的D点在底部横盘整理,今天也出现了明显的底部结束信号.老张预测这只股票未来一段时间的走势图会如图中虚线DEF段所示,且DEF段与ABC段关于直线l:
,并且从C点到今天的D点在底部横盘整理,今天也出现了明显的底部结束信号.老张预测这只股票未来一段时间的走势图会如图中虚线DEF段所示,且DEF段与ABC段关于直线l:![]() 对称,点B,D的坐标分别是
对称,点B,D的坐标分别是![]() .
.
![]() 请你帮老张确定a,
请你帮老张确定a,![]() ,
,![]() 的值,并写出ABC段的函数解析式;
的值,并写出ABC段的函数解析式;
![]() 如果老张预测准确,且今天买入该只股票,那么买入多少天后股价至少是买入价的两倍?
如果老张预测准确,且今天买入该只股票,那么买入多少天后股价至少是买入价的两倍?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某闯关游戏共有两关,游戏规则:先闯第一关,当第一关闯过后,才能进入第二关,两关都闯过,则闯关成功,且每关各有两次闯关机会.已知闯关者甲第一关每次闯过的概率均为![]() ,第二关每次闯过的概率均为
,第二关每次闯过的概率均为![]() .假设他不放弃每次闯关机会,且每次闯关互不影响.
.假设他不放弃每次闯关机会,且每次闯关互不影响.
(1)求甲恰好闯关3次才闯关成功的概率;
(2)记甲闯关的次数为![]() ,求随机变量
,求随机变量![]() 的分布列和期望.。
的分布列和期望.。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理是类比推理的( )
A. 两条直线平行,同旁内角互补,如果![]() 和
和![]() 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则![]()
B. 由平面三角形的性质,推测空间四边形的性质
C. 某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员.
D. 一切偶数都能被2整除,![]() 是偶数,所以
是偶数,所以![]() 能被2整除.
能被2整除.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设曲线![]() (
(![]() ),
),![]() 是直线
是直线![]() 上的任意一点,过
上的任意一点,过![]() 作
作![]() 的切线,切点分别为
的切线,切点分别为![]() 、
、![]() ,记
,记![]() 为坐标原点.
为坐标原点.
(1)设![]() ,求
,求![]() 的面积;
的面积;
(2)设![]() 、
、![]() 、
、![]() 的纵坐标依次为
的纵坐标依次为![]() 、
、![]() 、
、![]() ,求证:
,求证:![]() ;
;
(3)设点![]() 满足
满足![]() ,是否存在这样的点
,是否存在这样的点![]() ,使得
,使得![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在
在![]() 上?若存在,求出
上?若存在,求出![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:x2≤5x-4,q:x2-(a+2)x+2a≤0.
(1)若p是真命题,求对应x的取值范围;
(2)若p是q的必要不充分条件,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年某地区初中升学体育考试规定:考生必须参加长跑、掷实心球、1分钟跳绳三项测试.某学校在九年级上学期开始,就为掌握全年级学生1分钟跳绳情况,抽取了100名学生进行测试,得到下面的频率分布直方图.
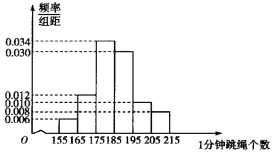
(Ⅰ)规定学生1分钟跳绳个数大于等于185为优秀.若在抽取的100名学生中,女生共有50人,男生1分钟跳绳个数大于等于185的有28人.根据已知条件完成下面的![]() 列联表,并根据这100名学生的测试成绩,判断能否有99%的把握认为学生1分钟跳绳成绩是否优秀与性别有关.
列联表,并根据这100名学生的测试成绩,判断能否有99%的把握认为学生1分钟跳绳成绩是否优秀与性别有关.
1分钟跳绳成绩 | 优秀 | 不优秀 | 合计 |
男生人数 | 28 | ||
女生人数 | 100 | ||
合计 | 100 |
(Ⅱ)根据往年经验,该校九年级学生经过训练,正式测试时每人1分钟跳绳个数都有明显进步.假设正式测试时每人1分钟跳绳个数都比九年级上学期开始时增加10个,全年级恰有2000名学生,若所有学生的1分钟跳绳个数![]() 服从正态分布
服从正态分布![]() ,用样本数据的平均值和标准差估计
,用样本数据的平均值和标准差估计![]() 和
和![]() ,各组数据用中点值代替),估计正式测试时1分钟跳绳个数大于183的人数(结果四舍五入到整数
,各组数据用中点值代替),估计正式测试时1分钟跳绳个数大于183的人数(结果四舍五入到整数
附: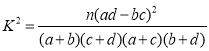 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=2sin(ωx+φ)(ω>0,|φ|<![]() )的一个零点为
)的一个零点为![]() ,其图象距离该零点最近的一条对称轴为x=
,其图象距离该零点最近的一条对称轴为x=![]() .
.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若关于x的方程f(x)+log2k=0在x∈[![]() ,
,![]() ]上恒有实数解,求实数k的取值范围.
]上恒有实数解,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com