
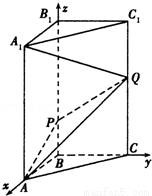
(本小题12分) 如图,在边长为12的正方形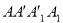 中,点B、C在线段AA′上,且AB=3,BC=4.作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q. 现将该正方形沿BB1,CC1折叠,使得
中,点B、C在线段AA′上,且AB=3,BC=4.作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q. 现将该正方形沿BB1,CC1折叠,使得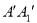 与AA1重合,构成如图(2)所示的三棱柱ABC-A1B1C1.
与AA1重合,构成如图(2)所示的三棱柱ABC-A1B1C1.
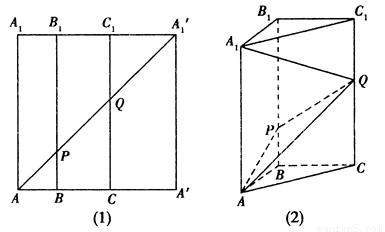
(1)在三棱柱ABC-A1B1C1中,求证:AP⊥BC;
(2)在三棱柱ABC-A1B1C1中,连接AQ与A1P,求四面体AA1QP的体积;
(3)在三棱柱ABC- A1B1C1中,求直线 PQ与直线AC所成角的余弦值.
(1)详见解析;(2)24;(3)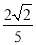 .
.
【解析】
试题分析:(1)由勾股定理逆定理,可得BC⊥AB,再由线面垂直的判定定理和性质定理,即可得证;
(2)求出三角形APA1的面积和Q到面APA1距离,运用棱锥的体积公式,即可得到;
(3)以BA,BC,BB1为x,y,z轴,建立空间直角坐标系,求出向量AC,PQ的坐标,由向量的夹角公式,即可得到.
试题解析:(1)因为AB=3,BC=4,
所以图(2)中AC=5,
从而有AC2=AB2+BC2,即BC⊥AB.
又因为BC⊥BB1,
所以BC⊥平面ABB1A1,
则AP⊥BC;
(2)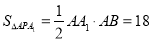 ,
,
由于CQ∥面APA1且BC⊥面APA1,
所以Q到面APA1距离就是BC的长4,
所以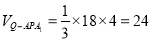 ;
;
(3)以BA,BC,BB1为x,y,z轴,建立如图空间直角坐标系,
则A(3,0,0)、C(0,4,0)、P(0,0,3)、Q(0,4,7).
所以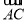 =(﹣3,4,0),
=(﹣3,4,0),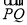 =(0,4,4),
=(0,4,4),
设直线AC与直线PQ所成角为θ,
则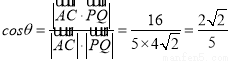 .
.
考点:空间直线与平面的位置关系;线面平行和垂直的判定和性质定理及运用;棱锥的体积公式;异面直线所成的角的求法.


科目:高中数学 来源:2014-2015学年江苏省淮安市高三数学第一次调研测试理科数学试卷(解析版) 题型:填空题
如图,在正三棱柱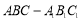 中,若各条棱长均为2,且M为
中,若各条棱长均为2,且M为 的中点,则三棱锥
的中点,则三棱锥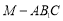 的体积是 .
的体积是 .

查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省淮安市高三数学第一次调研测试理科数学试卷(解析版) 题型:填空题
若采用系统抽样方法从420人中抽取21人做问卷调查,为此将他们随机编号为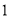 ,
,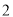 , ,
, ,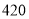 ,则抽取的
,则抽取的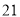 人中,编号在区间
人中,编号在区间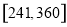 内的人数是 .
内的人数是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高二上学期期中考试理科数学试卷(解析版) 题型:填空题
半径为5的球内包含有一个圆台,圆台的上、下两个底面都是球的截面圆,半径分别为3和4. 则该圆台体积的最大值为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高二上学期期中考试理科数学试卷(解析版) 题型:选择题
下列有关命题的说法错误的是 ( )
A.对于命题 :
: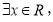 使得
使得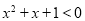 . 则
. 则
 :
: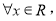 均有
均有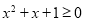 .
.
B.“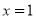 ”是“
”是“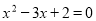 ”的充分不必要条件.
”的充分不必要条件.
C.命题“若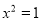 ,则
,则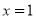 ”的否命题为:“若
”的否命题为:“若 ,则
,则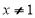 ”.
”.
D.命题“若 ,则
,则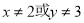 ”是假命题.
”是假命题.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省高二上学期期中考试理科数学试卷(解析版) 题型:填空题
某单位有职工200名,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按
1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,…,196-200号).若第5组抽出的号码
为22,则第10组抽出的号码应是_________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中练习文科数学试卷(解析版) 题型:解答题
如图,正方体 的棱长为1,线段
的棱长为1,线段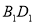 上有两个动点E,F,且
上有两个动点E,F,且 ,则下列结论中错误的是( )
,则下列结论中错误的是( )

A.
B.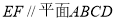
C.三棱锥 的体积为定值
的体积为定值
D.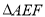 的面积与
的面积与 的面积相等
的面积相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com