（2014•安徽模拟）若2m+4n＜2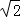
，则点（m，n）必在（ ）
A.直线x+y=1的左下方 B.直线x+y=1的右上方
C.直线x+2y=1的左下方 D.直线x+2y=1的右上方
一课一练课时达标系列答案
期末宝典单元检测分类复习卷系列答案科目：高中数学 来源：[同步]2014年新人教B版选修4-5 1.3绝对值不等式的解法练习卷（解析版） 题型：选择题
（2014•南昌一模）已知函数f（x）=|2x﹣a|+a．若不等式f（x）≤6的解集为{x|﹣2≤x≤3}，则实数a的值为（ ）
A.1 B.2 C.3 D.4
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教B版选修4-5 1.3绝对值不等式的解法练习卷（解析版） 题型：选择题
（2014•河西区三模）已知不等式|y+4|﹣|y|≤2x+
对任意实数x，y都成立，则常数a的最小值为（ ）
A.1 B.2 C.3 D.4
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教B版选修4-5 1.2基本不等式练习卷（解析版） 题型：选择题
（2014•广州一模）已知x＞﹣1，则函数y=x+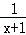
的最小值为（ ）
A.﹣1 B.0 C.1 D.2
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教B版选修4-5 1.2基本不等式练习卷（解析版） 题型：选择题
（2014•兴安盟一模）x、y满足约束条件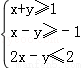
，若目标函数z=ax+by（a＞0，b＞0）的最大值为7，则
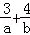的最小值为（ ）
A.14 B.7 C.18 D.13
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教B版选修2-1 2.1曲线与方程练习卷（解析版） 题型：选择题
（2014•开封二模）若曲线f（x）=acosx与曲线g（x）=x2+bx+1在交点（0，m）处有公切线，则a+b=（ ）
A.1 B.2 C.3 D.4
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教B版选修2-1 2.1曲线与方程练习卷（解析版） 题型：选择题
（2014•青岛一模）曲线y=x3﹣2x在点（1，﹣1）处的切线方程是（ ）
A.x﹣y﹣2=0 B.x﹣y+2=0 C.x+y+2=0 D.x+y﹣2=0
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教B版选修1-2 1.1独立性检验练习卷（解析版） 题型：选择题
（2014•泰安一模）为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老人，结果如表：
性 别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
由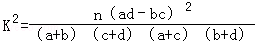
算得，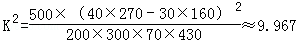
附表：
P（K2≥k） | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表，得到的正确结论是（ ）
A.在犯错误的概率不超过0.1%的前提下，认为“需要志愿者提供帮助与性别有关”
B.在犯错误的概率不超过0.1%的前提下，认为“需要志愿者提供帮助与性别无关”
C.有99%以上的把握认为“需要志愿者提供帮助与性别有关”
D.有99%以上的把握认为“需要志愿者提供帮助与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，再结合题意并化简2m+2n＜2，由指数函数的单调性求解此不等式，再解集转化为几何意义．
=2
，∴2
＜2
的最小值是（ ）
B.
C.3 D.4