
 如图所示,双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的左支上有一点P,∠F1PF2=
如图所示,双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的左支上有一点P,∠F1PF2=| π |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 3 |
| c |
| a |
| 2 |
| 3 |
| 3x2 |
| 2 |
| y2 |
| 2 |


科目:高中数学 来源: 题型:
 (2012•红桥区一模)如图所示,双曲线
(2012•红桥区一模)如图所示,双曲线| x2 |
| 16 |
| y2 |
| 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•宣武区一模)在面积为9的△ABC中,tan∠BAC=-
(2008•宣武区一模)在面积为9的△ABC中,tan∠BAC=-| 4 |
| 3 |
| CD |
| DB |
| DE |
| DF |
查看答案和解析>>
科目:高中数学 来源: 题型:
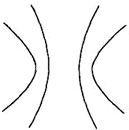 已知定圆O1、O2的半径分别为r1、r2,圆心距|O1O2|=2,动圆C与圆O1、O2都相切,圆心C的轨迹为如图所示的两条双曲线,两条双曲线的离心率分别为e1、e2,则
已知定圆O1、O2的半径分别为r1、r2,圆心距|O1O2|=2,动圆C与圆O1、O2都相切,圆心C的轨迹为如图所示的两条双曲线,两条双曲线的离心率分别为e1、e2,则| e1+e2 |
| e1e2 |
| A、r1+r2 |
| B、r1和r2中的较大者 |
| C、r1和r2中的较小者 |
| D、|r1-r2| |
查看答案和解析>>
科目:高中数学 来源:2007年江苏省丹阳高级中学高三模拟试题一、数学 题型:013
如图所示,在△ABC中,∠CAB=∠CBA=30°,AC、BC上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为
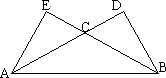
A.![]()
B.1
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年鄞州中学模拟理)(15分) 在面积为9的![]() 中,
中,![]() ,且
,且![]() 。现建立以A点为坐标原点,以
。现建立以A点为坐标原点,以![]() 的平分线所在直线为x轴的平面直角坐标系,如图所示。
的平分线所在直线为x轴的平面直角坐标系,如图所示。
(1) 求AB、AC所在的直线方程;
(2) 求以AB、AC所在的直线为渐近线且过点D的双曲线的方程;
(3)过D分别作AB、AC所在直线的垂线DF、DE(E、F为垂足),求![]() 的值。
的值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com